【题目】A市有近20年的马拉松比赛历史,过去全程马拉松名额一直相对较少。而近几年,这一现状大大改变,很多想参加全程马拉松(简称全马)的跑者报不上名。所以该城市近两年也大幅增加“全马”的名额。2017年,参加“全马”的人数比“半马”的人少,但是2018年,2019年参加“全马”的人数呈上升趋势,且每年比前一年均增加25%(即2018年比2017年增加25%,2019年比2018年增加25%),2019年,有12500名“全马”参赛者。
(1)求2017年、2018年“全马”参赛人数;
(2)据赞助食物的某商家反映:2017年与2018年该商家分别给参加“全马”和“半马”的参赛者提供了不同价格的食物,每个“全马”参赛者获得的食物价值高于“半马”参赛者,2017年,商家提供食物共用去22万元;这两年商家是按同一个标准分别给“全马”和“半马”参赛者提供食物(人太多,标准不可轻易提高),即使这样,2018年,虽然参加马拉松比赛的总人数与2017年一样多,但是由于“全马”参赛者人数刚好与“半马”参赛者人数调换了,赞助商比2017年多提供了p万元的食物;商家发现这p万元的食物刚好可以供400名“全马”参赛者和400名“半马”参赛者享用。求p的值。
参考答案:
【答案】(1)8000人、10000人;(2)1.
【解析】
(1)设2017年参加全马有![]() 人,根据每年比前一年均增加25%,2019年有12500名“全马”参赛者列方程求解即可;
人,根据每年比前一年均增加25%,2019年有12500名“全马”参赛者列方程求解即可;
(2)设赞助商给每个全马,半马参赛者提供的食物价格分别是![]() 万元,
万元, ![]() 万元,根据题意列方程组求解即可.
万元,根据题意列方程组求解即可.
解 :(1)设2017年参加全马有![]() 人,根据题意得
人,根据题意得
由![]() ,
,
得![]() ,那么
,那么![]() ,
,
所以2017年、2018年参加全马分别为8000人、10000人;
(2)设赞助商给每个全马,半马参赛者提供的食物价格分别是![]() 万元,
万元, ![]() 万元,则
万元,则
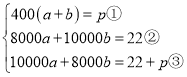 ,
,
由![]() +
+![]() ,得
,得
![]() ④,
④,
由![]() 得
得![]()
![]() ,代入④,得,
,代入④,得, ![]() ,
,
解得
![]() ,
,
所以p值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD//BC,
 ,
, ,
, ,
, ,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动;动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动,其中一点到达终点时,则两点同时停止运动.设运动的时间为t秒,当△MNB为等腰直角三角形时,t的值是_______.
,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动;动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动,其中一点到达终点时,则两点同时停止运动.设运动的时间为t秒,当△MNB为等腰直角三角形时,t的值是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题.
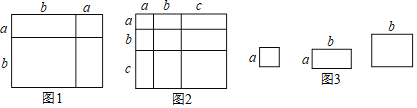
(1)写出图2中所表示的数学等式 ;
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2;
(4)利用(1)中得到的结论,直接写出代数式
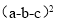 展开之后的结果:
展开之后的结果: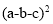 =
= -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.(1)求证:AB=CE;
(2)若
 ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在△ABC中,∠BAC=90,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D. A.E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D. A.E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。
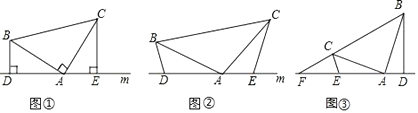
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强课外阅读,开阔视野,我校开展了“书香校园”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制成如下频数分布表和不完整的频数直方
图:


请根据图表信息回答下列问题:
(1)频数分布表中的a=_______,b=_______;
(2)将频数直方图补充完整;
(3)全校共有学生1200人,若规定阅读时间超过2小时则评为“优秀阅读员”,请估计能评为“优秀阅读员”的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙
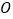 的直径,过点A作⊙
的直径,过点A作⊙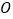 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙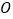 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.(1)求证:
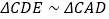 ;
;(2)若AB=2,
 ,求AE的长.
,求AE的长. 
相关试题

