【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
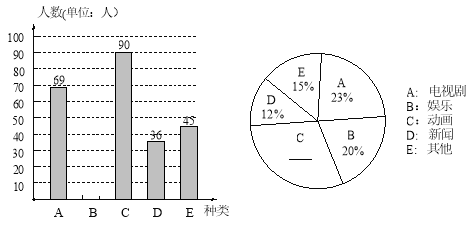
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
参考答案:
【答案】(1)300人;(2)补全统计图参见解析;43.2°;(3)460人.
【解析】
试题分析:(1)只要用部分人数除以部分所占的百分比即得本次调查的学生人数;(2)用总人数乘以B所站的百分比就是B的人数,即可补全条形统计图;用90除以总人数,化成百分数,即可补全扇形统计图;用360度乘以新闻所占的百分比就是新闻节目在扇形统计图中所占圆心角的度数;(3)用样本估计总体,即用2000人乘以电视剧所占的百分数就是该校喜爱电视剧节目的人数.
试题解析:(1)69÷23%=300(人),∴本次共调查300人.(2)300×20%=60(人)∴B的人数是60人,补全对应条形统计图;90÷300=30%,∴C占扇形的30%,对应填上百分数;360°×12%=43.2°,∴新闻节目在扇形统计图中所占圆心角的度数为43.2° ;(3)2000×23%=460(人),∴估计该校喜爱电视剧节目的人数是460人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
59
96
116
290
480
601
摸到白球的频率
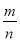
a
0.64
0.58
b
0.60
0.601
(1)上表中的a= ;b=
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)试估算口袋中黑、白两种颜色的球各有多少只?
-
科目: 来源: 题型:
查看答案和解析>>【题目】深化理解:
新定义:对非负实数x “四舍五入”到个位的值记为
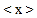 ,
,即:当n为非负整数时,如果
 ;
;反之,当n为非负整数时,如果
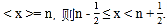
例如:<0> = <0.48> = 0,<0.64> = <1.49> = 1,<2> = 2,<3.5> = <4.12> = 4,……
试解决下列问题:
(1)填空:①
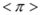 =________(
=________( 为圆周率); ②如果
为圆周率); ②如果 的取值范围为____________________.
的取值范围为____________________.(2)若关于x的不等式组
 的整数解恰有3个,求a的取值范围.
的整数解恰有3个,求a的取值范围.(3)求满足
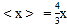 的所有非负实数x的值.
的所有非负实数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的序号有 .
①在Rt△ABC中,∠C=90°,CD为AB边上的中线,且CD=2,则AB=4;
②八边形的内角和度数为1080°;
③2、3、4、3这组数据的方差为0.5;
④分式方程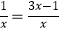 的解为x=
的解为x=  ;
;
⑤已知菱形的一个内角为60°,一条对角线为2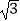 ,则另一条对角线长为2.
,则另一条对角线长为2. -
科目: 来源: 题型:
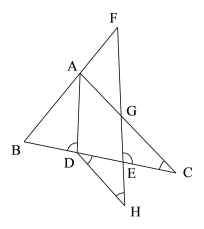
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,AD∥EF.
(1)求证:∠BDA+∠CEG=180°;
(2)若点H在FE的延长线上,且∠F=∠H,则∠EDH与∠C相等吗,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
(2)如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标;
(3)如图2,M为x轴负半轴上一点,且∠CBM=∠CMB,N是x轴正半轴上一动点,∠MCN的平分线CD交BM的延长线于点D,在点N运动的过程中,
 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为 .

相关试题

