【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
(2)如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标;
(3)如图2,M为x轴负半轴上一点,且∠CBM=∠CMB,N是x轴正半轴上一动点,∠MCN的平分线CD交BM的延长线于点D,在点N运动的过程中,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.

参考答案:
【答案】(1)B(-5,-3);(2)点P的坐标为(-3,0)或(0,-![]() );(3)
);(3)![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据已知条件易得点B的坐标为(-5,-3);
(2)根据题意分点P在边OA上和点P在边OC上两种情况结合已知条件进行分析解答即可;
(3)如图3,延长BC至点F,过点M作ME∥CD交BC于点E,结合已知条件可得∠D=∠BME=∠CMB-∠EMC=![]() ∠MCF-
∠MCF-![]() ∠NCM,在结合∠CNM=∠NCF=∠MCF-∠NCM即可得到∠CNM=2∠D,由此即可得到
∠NCM,在结合∠CNM=∠NCF=∠MCF-∠NCM即可得到∠CNM=2∠D,由此即可得到![]() =
=![]() .
.
(1)∵四边形OABC为长方形,OA=5,OB=3,且点B在第三象限,
∴B(-5,-3),
(2)若过点B的直线BP与边OA交于点P,依题意可知:![]() ×AB×AP=
×AB×AP=![]() ×OA×OC,
×OA×OC,
即![]() ×3×AP=
×3×AP=![]() ×5×3,∴AP=2,
×5×3,∴AP=2,
∵OA=5,
∴OP=3,
∴P(-3,0).
若过点B的直线BP与边OC交于点P,依题意可知:![]() ×BC×PC=
×BC×PC=![]() ×OA×OC,
×OA×OC,
即![]() ×5×PC=
×5×PC=![]() ×5×3,∴PC=
×5×3,∴PC=![]() ∵OC=3,∴OP=
∵OC=3,∴OP=![]() ,∴P(0,-
,∴P(0,-![]() ).
).
综上所述,点P的坐标为(-3,0)或(0,-![]() ).
).
(3)如图3,延长BC至点F,过点M作ME∥CD交BC于点E,
∵四边形OABC为长方形,
∴OA∥BC.
∴∠CBM=∠AMB,∠AMC=∠MCF.
∵∠CBM=∠CMB,∠MCF=∠CBM+∠CMB,
∴∠CMB=![]() ∠MCF,
∠MCF,
∵ME∥CD,
∴∠EMC=
又∵CD平分∠MCN,
∴∠EMC=![]() ∠NCM,
∠NCM,
∴∠D=∠BME=∠CMB-∠EMC=![]() ∠MCF-
∠MCF-![]() ∠NCM,
∠NCM,
又∵∠CNM=∠NCF=∠MCF-∠NCM,
∴∠CNM=2∠D,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的序号有 .
①在Rt△ABC中,∠C=90°,CD为AB边上的中线,且CD=2,则AB=4;
②八边形的内角和度数为1080°;
③2、3、4、3这组数据的方差为0.5;
④分式方程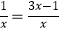 的解为x=
的解为x=  ;
;
⑤已知菱形的一个内角为60°,一条对角线为2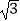 ,则另一条对角线长为2.
,则另一条对角线长为2. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
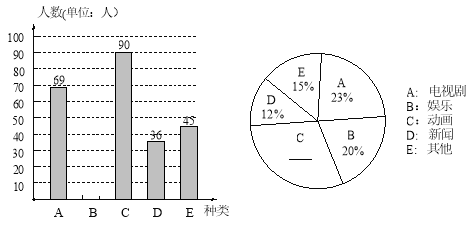
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
-
科目: 来源: 题型:
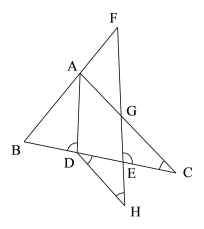
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,AD∥EF.
(1)求证:∠BDA+∠CEG=180°;
(2)若点H在FE的延长线上,且∠F=∠H,则∠EDH与∠C相等吗,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
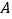 在数轴上对应的数为
在数轴上对应的数为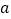 ,点
,点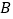 对应的数为
对应的数为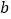 ,且
,且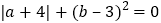 .
.
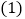 则
则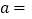 ________,
________,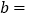 ________;并将这两个数在数轴上所对应的点
________;并将这两个数在数轴上所对应的点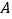 ,
,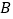 表示出来;
表示出来;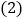 数轴上在
数轴上在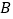 点右边有一点
点右边有一点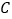 到
到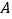 、
、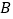 两点的距离和为
两点的距离和为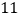 ,若点
,若点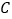 的数轴上所对应的数为
的数轴上所对应的数为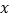 ,求
,求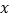 的值;
的值;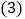 若点
若点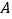 ,点
,点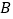 同时沿数轴向正方向运动,点
同时沿数轴向正方向运动,点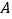 运动的速度为
运动的速度为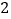 单位/秒,点
单位/秒,点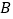 运动的速度为
运动的速度为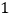 单位/秒,若
单位/秒,若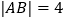 ,求运动时间
,求运动时间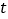 的值.
的值.(温馨提示:
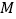 、
、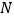 之间距离记作
之间距离记作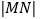 ,点
,点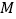 、
、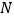 在数轴上对应的数分别为
在数轴上对应的数分别为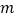 、
、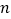 ,则
,则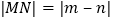 .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】国际足球比赛对足球的质量有严格的要求,比赛所用足球上标有:430±20(g).请问:
(1)比赛所用足球的标准质量是多少?符合比赛所用足球质量的合格范围是多少?
(2)组委会随机抽查了8只足球的质量,高于标准质量记为正,低于标准质量记为负,结果分别是:﹣15g,+12g,﹣24g,﹣6g,+13g,﹣5g,+22g,﹣9g,求这8只足球质量的合格率.
(足球质量的合格率=
 )
)
相关试题

