【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
参考答案:
【答案】(1)在公司的东边10千米处;(2)共耗油4.8升;(3)共收到车费68元.
【解析】
(1)由题意把接送![]() 批客人的行驶路程相加,并进行计算即可;
批客人的行驶路程相加,并进行计算即可;
(2)根据题意先计算出总行驶路程,再乘以出租车每千米耗油![]() 升即可求出在这过程中共耗油多少升;
升即可求出在这过程中共耗油多少升;
(3)根据题意分别计算出各个批次所收到的车费,再进行相加即可.
解:(1)5+2+(-4)+(-3)+10=10(km).
由题意可知规定向东为正,向西为负,
答:接送完第5批客人后,该驾驶员在公司的东边10千米处.
(2)由题意出租车每千米耗油![]() 升可得:
升可得:
(5+2+|-4|+|-3|+10)×0.2=24×0.2=4.8(升).
答:在这个过程中共耗油4.8升.
(3)[10+(5-3)×1.8]+10+[10+(4-3)×1.8]+10+[10+(10-3)×1.8]=68(元).
答:在这个过程中该驾驶员共收到车费68元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且
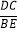 =
=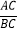 =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
=m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.(1)如图1,过点E作EH⊥AB于点H,连结DH.
①求证:四边形DHEC是平行四边形;
②若m=
 ,求证:AE=DF;
,求证:AE=DF;(2)如图2,若m=
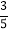 ,求
,求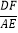 的值.
的值.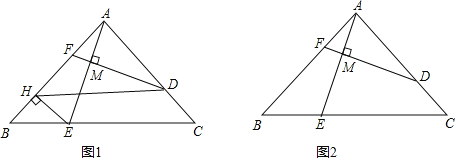
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,如果在正方形中画
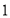 条纵线和
条纵线和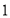 条横线,便把正方形分成
条横线,便把正方形分成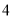 部分(如图①);如果在正方形中画
部分(如图①);如果在正方形中画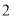 条纵线和
条纵线和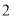 条横线,便把正方形分成
条横线,便把正方形分成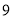 部分(如图②);如果在正方形中画
部分(如图②);如果在正方形中画 条纵线和
条纵线和 条横线,便把正方形分成
条横线,便把正方形分成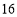 部分(如图③...如果在正方形中画
部分(如图③...如果在正方形中画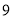 条纵线和
条纵线和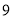 条横线.便把正方形分成( )部分
条横线.便把正方形分成( )部分
A.
 B.
B.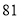 C.
C.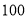 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正两位数的个位数字是a,十位数字比个位数字大2.
(1)列式表示这个两位数;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被22整除.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2
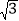 ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.(1)当OB=2时,求点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=
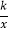 (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
(k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.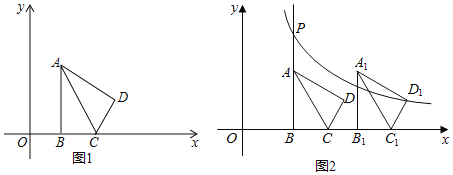
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
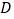 在反比例函数
在反比例函数 的图象上,过点
的图象上,过点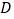 作
作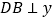 轴,垂足为
轴,垂足为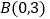 ,直线
,直线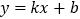 经过点
经过点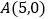 ,与
,与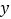 轴交于点
轴交于点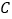 ,且
,且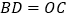 ,
,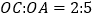 .
.
(1)求反比例函数
 和一次函数
和一次函数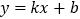 的表达式;
的表达式;(2)直接写出关于
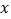 的不等式
的不等式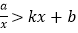 的解集.
的解集.
相关试题

