【题目】如下图。 
(1)问题 如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证: ![]() .
.
(2)探究 如图,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用 请利用(1)(2)获得的经验解决问题
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A.设点P的运动时间为t(秒),当以D为圆心,DC为半径的圆与AB相切时,求t的值.
参考答案:
【答案】
(1)证明:如图1,

∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠ADP=∠BPC,
∴△ADP∽△BPC,
∴ ![]()
(2)解:结论 ![]() 仍然成立.
仍然成立.
理由:如图2,

∵∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠ADP,
∴∠DPC+∠BPC=∠A+∠ADP.
∵∠DPC=∠A=∠B=θ,
∴∠BPC=∠ADP,
∴△ADP∽△BPC,
∴ ![]()
(3)解:如图3,

过点D作DE⊥AB于点E.
∵AD=BD=5,AB=6,
∴AE=BE=3.
由勾股定理可得DE=4.
∵以点D为圆心,DC为半径的圆与AB相切,
∴DC=DE=4,
∴BC=5﹣4=1.
又∵AD=BD,
∴∠A=∠B,
∴∠DPC=∠A=∠B.
∵AD=BD,
∴∠A=∠B,
∵∠BPD=∠A+∠ADP=∠DPC+∠BPC,∠DPC=∠A,
∴∠ADP=∠BPC,
∴△APD∽△BCP,
∴ ![]() ,
,
∴ADBC=APBP;
∴5×1=t(6﹣t),
解得:t1=1,t2=5,
∴t的值为1秒或5秒
【解析】(1)如图1,由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;(2)如图2,由∠DPC=∠A=∠B=θ可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;(3)如图3,过点D作DE⊥AB于点E,根据等腰三角形的性质可得AE=BE=3,根据勾股定理可得DE=4,由题可得DC=DE=4,则有BC=5﹣4=1.易证∠DPC=∠A=∠B.根据ADBC=APBP,就可求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.

(1)判断△ABC的形状:;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-102n×100×(-10)2n-1;
(2)[(-a)·(-b)2·a2b3c]2;
(3)(x3)2÷x2÷x-x3÷(-x)4·(-x4);
(4)(-9)3×
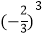 ×
× ;
;(5)xn+1·xn-1·x÷xm;
(6)a2·a3-(-a2)3-2a·(a2)3-2[(a3)3÷a3].
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y=﹣2x﹣2
(1)根据关系式画出函数的图象.
(2)求出图象与 x 轴、y 轴的交点 A、B 的坐标.
(3)求 A、B 两点间的距离.
(4)y 的值随 x 值的增大怎样变化?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( )

A. cm
cm
B. cm
cm
C. cm
cm
D.7πcm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABC中,
ABC中,  A=80
A=80 ,
,  ABC与
ABC与 ACD的平分线交于点A1,得
ACD的平分线交于点A1,得 A1;
A1;  A1BC与
A1BC与 A1CD的平分线相交于点A2,得
A1CD的平分线相交于点A2,得 A2;……;
A2;……;  A7BC与
A7BC与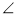 A7CD的平分线相交于点A8,得
A7CD的平分线相交于点A8,得 A8,则
A8,则 A8的度数为()
A8的度数为()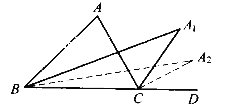
A.
 B.
B.  C.
C.  D.
D. 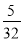
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22018+22019,①将等式两边同时乘2,得
2S=2+22+23+24+25+…+22019+22020,②
将②式减去①式,得2S-S=22020-1,
即S=22020-1,
则1+2+22+23+24+…+22019=22020-1.
请你仿照此法计算:
(1)1+2+22+23+24+…+210;
(2)1+3+32+33+34+…+3n(其中n为正整数).
相关试题

