【题目】如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是______(填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,-2],则其“抛物线三角形”的面积为________;
(3)若一条抛物线系数为[-1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB,如果存在,求出P点坐标,如果不存在,请说明理由.
参考答案:
【答案】(1)假;(2)![]() ;(3)y=-x2+2x 或y=-x2-2x;(4)P(1,1)或P(-1,-3)或P(1,-3)或(-1,1).
;(3)y=-x2+2x 或y=-x2-2x;(4)P(1,1)或P(-1,-3)或P(1,-3)或(-1,1).
【解析】(1)当△>0时,抛物线与x轴有两个交点,由此可得出结论;
(2)根据“抛物线三角形”定义得到![]() ,由此可得出结论;
,由此可得出结论;
(3)根据“抛物线三角形”定义得到y=-x2+2bx,它与x轴交于点(0,0)和(2b,0);
当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形,
由抛物线顶点为(b,b2),以及直角三角形斜边上的中线等于斜边的一半得到![]() ,解方程即可得到结论;
,解方程即可得到结论;
(4)分两种情况讨论:①当抛物线为y=-x2+2x 时,②当抛物线为y=-x2-2x 时.
(1)当△>0时,抛物线与x轴有两个交点,此时抛物线才有“抛物线三角形”,故此命题为假命题;
(2)由题意得:![]() ,令y=0,得:x=
,令y=0,得:x=![]() ,∴ S=
,∴ S=![]() =
=![]() ;
;
(3)依题意:y=-x2+2bx,它与x轴交于点(0,0)和(2b,0);
当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形.
∵y=-x2+2bx=![]() ,∴顶点为(b,b2),由直角三角形斜边上的中线等于斜边的一半得到:
,∴顶点为(b,b2),由直角三角形斜边上的中线等于斜边的一半得到:![]() ,∴
,∴![]() ,解得:b=0(舍去)或b=±1,
,解得:b=0(舍去)或b=±1,
∴y=-x2+2x 或y=-x2-2x.
(4)①当抛物线为y=-x2+2x 时.
∵△AOB为等腰直角三角形,且△BPQ∽△OAB,
∴△BPQ为等腰直角三角形,设P(a,-a2+2a),∴Q((a,0),
则|-a2+2a|=|2-a|,即![]() .
.
∵a-2≠0,∴![]() ,∴a=±1,∴P(1,1)或(-1, -3).
,∴a=±1,∴P(1,1)或(-1, -3).
②当抛物线为y=-x2-2x 时.
∵△AOB为等腰直角三角形,且△BPQ∽△OAB,
∴△BPQ为等腰直角三角形,设P(a,-a2-2a),∴Q((a,0),
则|-a2-2a|=|2+a|,即![]() .
.
∵a+2≠0,∴![]() ,∴a=±1,∴P(1,-3,)或(-1,1).
,∴a=±1,∴P(1,-3,)或(-1,1).
综上所述:P(1,1)或P(-1,-3)或P(1,-3,)或(-1,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
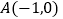 ,
,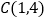 ,点
,点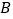 在
在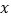 轴上,且
轴上,且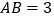 .
.(1)求点
 的坐标,并画出
的坐标,并画出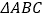 ;
;(2)求
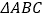 的面积;
的面积;(3)在
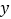 轴上是否存在点
轴上是否存在点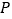 ,使以
,使以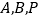 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点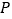 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.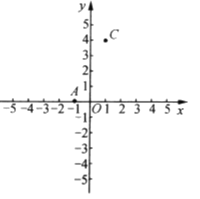
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
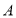 在数轴上对应的数为
在数轴上对应的数为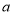 ,点
,点 对应的数为
对应的数为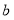 ,
, 为原点,且
为原点,且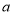 、
、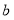 满足:
满足: .试解答下列问题:
.试解答下列问题:(1)求数轴上线段
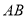 的长度;
的长度;(2)若点
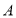 以每秒2个单位长度的速度沿数轴向右运动,则经过
以每秒2个单位长度的速度沿数轴向右运动,则经过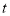 秒后点
秒后点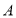 表示的数为 ;(用含
表示的数为 ;(用含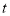 的代数式表示)
的代数式表示)(3)若点
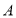 ,
, 都以每秒2个单位长度的速度沿数轴向右运动,而点
都以每秒2个单位长度的速度沿数轴向右运动,而点 不动,经过
不动,经过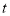 秒后其中一个点是一条线段的中点,求此时
秒后其中一个点是一条线段的中点,求此时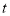 的值.
的值.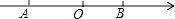
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是菱形
是菱形 边上的一动点,它从点
边上的一动点,它从点 出发沿在
出发沿在 路径匀速运动到点
路径匀速运动到点 ,设
,设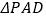 的面积为
的面积为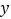 ,
,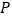 点的运动时间为
点的运动时间为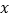 ,则
,则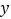 关于
关于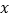 的函数图象大致为
的函数图象大致为
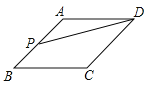
A.
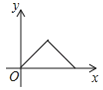 B.
B. 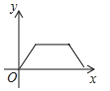
C.
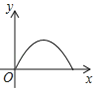 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一些蜂蜜,此时一只蚂蚁正好也在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,那么蚂蚁要吃到甜甜的蜂蜜所爬行的最短距离是( )

A.13B.14C.15D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A逆时针旋转α后,与△ADE构成位似图形,我们称与互为“旋转位似图形”。
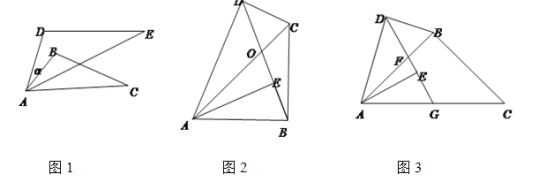
(1)知识理解:两个重合了一个顶点且边长不相等的等边三角形______(填“是”或“不是”)“旋转位似图形”;
如图1,△ABC和△ADE互为“旋转位似图形”,
①若α=26,∠B=100,∠E=29,则∠BAE=______;
②若AD=6,DE=8,AB=4,则BC=______;
(2)知识运用:
如图2,在四边形ABCD中,∠ADC=90,AE⊥BD于E,∠DAC=∠DBC,求证:△ACD和△ABE互为“旋转位似图形”;
(3)拓展提高:
如图3,△ABC为等腰直角三角形,点G为AC中点,点F是AB上一点,D是GF延长线上一点,点E在线段GF上,且△ABD与△AGE互为“旋转位似图形”,若AC=6,AD=2
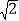 ,求出DE和BD的值。
,求出DE和BD的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-1)-(-3)
(2)
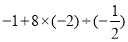
(3)
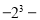 [(-56)×(
[(-56)×(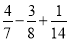 )+
)+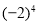 ]
] (4)
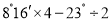
相关试题

