【题目】一个车队共有20辆小轿车,正以每小时36千米的速度在一条笔直的街道上匀速行驶,行驶时车与车的间隔均相等,甲停在路边等人,他发现该车队从第一辆车的车头到最后一辆的车尾经过自己身边共用了20秒的时间,假设每辆车的车长均为4.87米.
(1)求行驶时车与车的间隔为多少米?
(2)若乙在街道一侧的人行道上与车队同向而行,速度为![]() 米/秒,当第一辆车的车头到最后一辆车的车尾经过他身边共用了40秒,求
米/秒,当第一辆车的车头到最后一辆车的车尾经过他身边共用了40秒,求![]() 的值.
的值.
参考答案:
【答案】(1)车与车的间隔距离为5.4米;(2)![]() .
.
【解析】
(1)首先统一单位,由题意得等量关系:20辆小轿车的总长+20辆车之间的车距=20秒×车的行驶速度,根据等量关系列出方程,再解即可;
(2)计算出车队的总长度,再利用总路程为200m得出等式求出答案.
(1)设车与车的间隔距离为![]() 米,
米,
![]() ,
,
解得![]() .
.
答:行驶时车与车的间隔为5.4米.
(2)车队总长度:20×4.87+5.4×19=200(米),
![]() ,
,
解得![]() .
.
答:v的值为5..
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.

A. 0.5 B. 1 C. 1.5 D. 2
-
科目: 来源: 题型:
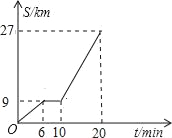
查看答案和解析>>【题目】如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题:
(1)汽车在前6分钟内的平均速度是 千米/小时,汽车在兴国服务区停了多长时间? 分钟;
(2)当10≤t≤20时,求S与t的函数关系式;
(3)规定:高速公路时速超过120千米/小时为超速行驶,试判断当10≤t≤20时,该汽车是否超速,说明理由.
-
科目: 来源: 题型:
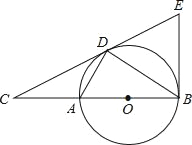
查看答案和解析>>【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.
-
科目: 来源: 题型:
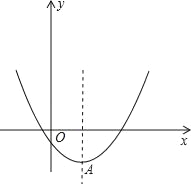
查看答案和解析>>【题目】已知二次函数y=x2﹣2mx+4m﹣8,
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A. 17cm B. 7cm C. 12cm D. 17cm或7cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探索新知)
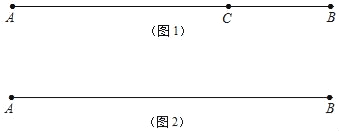
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
相关试题

