【题目】如图,在等边![]() 中,
中, ![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)连接![]() ,则
,则![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)若![]() ,求
,求![]() 的大小(用
的大小(用![]() 的式子表示)
的式子表示)
(2)用等式表示线段![]() 和
和![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
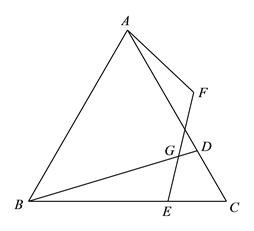
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() (3)
(3)![]() .
.
【解析】分析: (1)连接![]() ,
,![]() ,易证
,易证![]() 是等边三角形,则
是等边三角形,则![]() 根据点
根据点![]() 与点
与点![]() 关于
关于![]() 对称,则
对称,则![]() 根据等量代换可知
根据等量代换可知![]() ;
;
(2)根据![]() ,求出
,求出![]() .因为点
.因为点![]() 与点
与点![]() 关于
关于![]() 对称,得到
对称,得到![]() ,
,![]() .则
.则![]() .
.![]() ,
,![]() ,
,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上.根据圆周角定理有
为半径的圆上.根据圆周角定理有![]() .
.
(3)![]() .理由如下:连接
.理由如下:连接![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,证明
,证明![]() ,
,
得到![]() .根据
.根据![]() ,即可得到
,即可得到![]() .
.
(1)![]() ;
;
(2)如图:
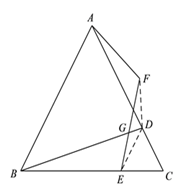
∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() .
.
∴![]() .
.
由(1)知![]() .
.
∴![]() ,
,![]() ,
,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上.
为半径的圆上.
∴![]() .
.
(3)![]() .理由如下:
.理由如下:
连接![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() .
.
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
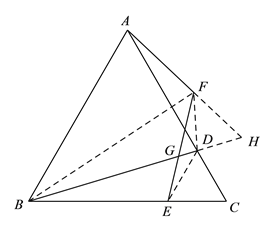
设![]() ,
,
则![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
由(2)知![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
四边形![]() 中,
中,![]() .
.
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
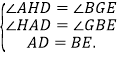
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
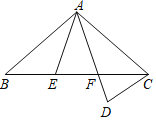
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校以“我最想去的社会实践地”为课题,开展了一次调查,从全校同学中随机抽取了部分同学进行调查,每位同学从“荪湖花海”、“保国寺”、“慈城古镇”、“绿色学校”中选取一项最想去的社会实践地,并将调查结果绘制成如下的统计图(部分信息未给出).

请根据统计图中信息,解答下列问题:
(1)该调查的样本容量为________,a=________%,b=________%,“荪湖花海”所对应扇形的圆心角度数为________度.
(2)补全条形统计图;
(3)若该校共有1600名学生,请估计全校最想去“绿色学校”的学生共有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边
 内一点,
内一点,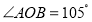 ,
,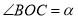 ,点D是等边△ABC外一点,∠OCD=60°,OC=OD,连接OD、AD.
,点D是等边△ABC外一点,∠OCD=60°,OC=OD,连接OD、AD.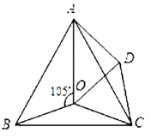
(1)求
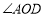 的度数(用含α的式子表示)
的度数(用含α的式子表示)(2)求证:
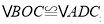 ;
;(3)探究:当α为多少度时,
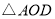 是等腰三角形.
是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒4个单位长度的速度向终点C移动,设移动时间为t秒.
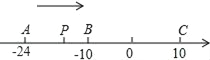
(1)用含t的代数式表示点P与A的距离:PA= ;点P对应的数是 ;
(2)动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,若P、Q同时出发,求:当点P运动多少秒时,点P和点Q间的距离为8个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小明把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域内的数字(若指针在分格线上,则重转一次,直到指针指向某一区域内为止).
(1)请用列表法或画树形图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之积为负数的概率.
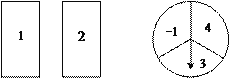
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图某同学将一个正方形纸片剪去一个宽为
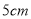 的长条后,再从剩下的长方形纸片上剪去一个宽为
的长条后,再从剩下的长方形纸片上剪去一个宽为 的长条.若两次剪下的长条面积正好相等,则每一个长条的面积为( )
的长条.若两次剪下的长条面积正好相等,则每一个长条的面积为( )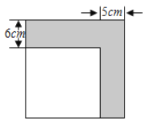
A.
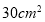 B.
B.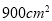 C.
C.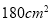 D.
D.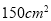
相关试题

