【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒4个单位长度的速度向终点C移动,设移动时间为t秒.
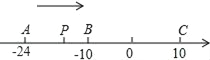
(1)用含t的代数式表示点P与A的距离:PA= ;点P对应的数是 ;
(2)动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,若P、Q同时出发,求:当点P运动多少秒时,点P和点Q间的距离为8个单位长度?
参考答案:
【答案】(1) 4t;﹣24+4t;(2) 2秒或![]() 秒
秒
【解析】
(1)根据题意容易得出结果;
(2)需要分类讨论:当点P在Q的左边和右边列出方程解答.
解:(1)PA=4t;点P对应的数是﹣24+4t;
故答案为:4t;﹣24+4t;
(2)
分两种情况:
当点P在Q的左边:4t+8=14+t,
解得:t=2;
当点P在Q的右边:4t=14+t+8,
解得:t=![]() ,
,
综上所述:当点P运动2秒或![]() 秒时,点P和点Q间的距离为8个单位长度.
秒时,点P和点Q间的距离为8个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD是任意四边形,AC与BD交于点O.试说明:AC+BD>
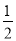 (AB+BC+CD+DA).
(AB+BC+CD+DA).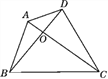
解:在△OAB中有OA+OB>AB,
在△OAD中有______________,
在△ODC中有______________,
在△________中有______________,
∴OA+OB+OA+OD+OD+OC+OB+OC>AB+AD+CD+BC,
即________________________.
∴AC+BD>
 (AB+BC+CD+DA).
(AB+BC+CD+DA). -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)7(2x–1)–3(4x–1)=4(3x+2)–1;
(2)
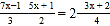 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
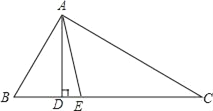
-
科目: 来源: 题型:
查看答案和解析>>【题目】取一张矩形的纸片进行折叠,具体操作过程如下: 第一步:先把矩形ABCD对折,折痕为MN,如图(1);
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,得Rt△AB′E,如图(2);
第三步:沿EB′线折叠得折痕EF,如图(3).
若AB=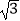 ,则EF的值是( )
,则EF的值是( )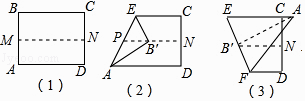
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( )
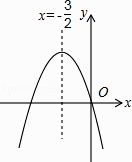
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )

A. cm2
cm2
B. cm2
cm2
C.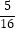 cm2
cm2
D. cm2
cm2
相关试题

