【题目】在今年“五一”小长假期间,某学校团委要求学生参加一项社会调查活动,八年级学生小明想了解他所居住的小区500户居民的家庭收入情况,从中随机调查了本小区一定数量居民家庭的收入情况(收入取整数,单位:元),并将调查的数据绘制成如下直方图和扇形图,根据图中提供的信息,解答下列问题:
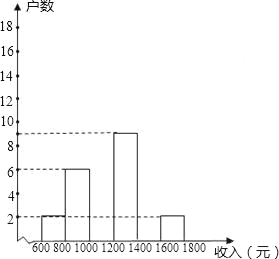
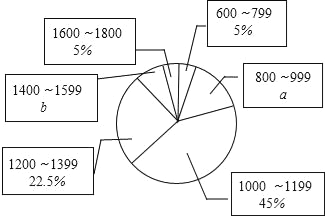
(1)这次共调查了 个家庭的收入,a= ,b= ;
(2)补全频数分布直方图,样本的中位数落在第 个小组;
(3)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
(4)在第1组和第5组的家庭中,随机抽取2户家庭,求这两户家庭人均月收入差距不超过200元的概率.
参考答案:
【答案】(1)这次共调查了40个家庭;a=15%,b=7.5%;(2)三;(3)估计该居民小区家庭收入较低(不足1000元)的户数大约有100户;(4)这两户家庭人均月收入差距不超过200元的概率为![]() .
.
【解析】【试题分析】
(1)求数据总数,等于频数除以对应的百分比;
(2)考查一组数据的中位数,按照从小到大或者从大到小的顺序,正中间的数据落到的小组,即为所求.
(3)用样本估计总体,即可;
(4)画树状图求概率.
【试题解析】
(1)2÷5%=40(个),所以这次共调查了40个家庭;
a=6÷40=15%,
第三组的家庭个数=40×45%=18(个),
b=(40﹣2﹣6﹣18﹣9﹣2)÷40=7.5%,
(2)第20个数和第21个数都落在第三组,所以样本的中位数落在第三个小组,
如图,
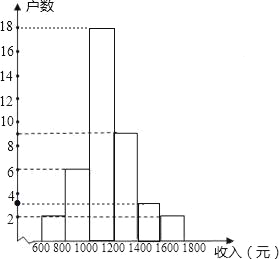
故答案为40,15%,7.5%;三;
(3)500×(5%+15%)=100(户),
所以估计该居民小区家庭收入较低(不足1000元)的户数大约有100户;
(4)设第1组的2户用A、B表示,第5组的3户用a、b、c表示,
画树状图为:

共有20种等可能的结果数,其中这两户家庭人均月收入差距不超过200元的结果数为8,
所以这两户家庭人均月收入差距不超过200元的概率=![]() =
=![]() .
.
-
科目: 来源: 题型:
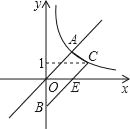
查看答案和解析>>【题目】如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,﹣4),则四边形AOBC的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
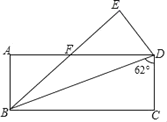
A. 62°B. 56°C. 31°D. 28°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明得到育才学校数学课外兴趣小组成员的年龄情况统计如下表:
年龄(岁)
13
14
15
16
人数(人)
5
15
x
10-x
那么对于不同x的值,则下列关于年龄的统计量不会发生变化的是( )
A. 众数,中位数B. 中位数,方差C. 平均数,中位数D. 平均数,方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
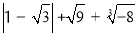
(2)已知:如图,在△ABC中,AB=AC,点D、E、F分别是△ABC各边的中点,求证:四边形AEDF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点A,B的横坐标分别为﹣1,3.与y轴负半轴交于点C,在下面四个结论中:①ac<0;②2a﹣b=0;③a+b+c>0;④c=﹣3a.其中正确的结论有( )
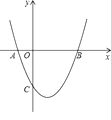
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

