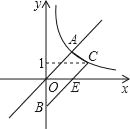
【题目】如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,﹣4),则四边形AOBC的面积为_____.
参考答案:
【答案】2![]() +10.
+10.
【解析】因为AO∥BC,上底边OA在直线y=x上,
则可设BC的解析式为y=x+b,
将B(0,﹣4)代入上式得,b=﹣4,
BC的解析式为y=x﹣4.
把y=1代入y=x﹣4,得x=5,C点坐标为(5,1),
则反比例函数解析式为y=![]() ,
,
将它与y=x组成方程组得:![]() ,
,
解得x=![]() ,x=﹣
,x=﹣![]() (负值舍去).
(负值舍去).
代入y=x得,y=![]() ,
,
A点坐标为(![]() ,
,![]() ),
),
OA=![]() =
=![]() ,
,
BC=![]() =5
=5![]() ,
,
∵BC的解析式为y=x﹣4,
∴E(4,0),
∵B(0,﹣4),
∴BE=![]() =4
=4![]() ,
,
设BE边上的高为h,
![]() h×
h×![]() =4×4×
=4×4×![]() ,
,
解得:h=2![]() ,
,
则梯形AOBC高为:2![]() ,
,
梯形AOBC面积为:![]() ×2
×2![]() ×(
×(![]() +5
+5![]() )=2
)=2![]() +10,
+10,
故答案为:2![]() +10.
+10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标为(a,6)(其中a<-
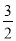 ),射线OA与反比例函数
),射线OA与反比例函数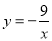 的图像交于点P,点B,C分别在函数
的图像交于点P,点B,C分别在函数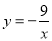 的图像上,且AB∥x轴,AC∥y轴,连接BP,CP.
的图像上,且AB∥x轴,AC∥y轴,连接BP,CP.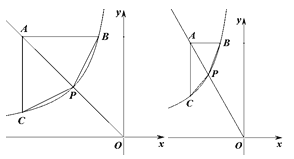
(1)当a=-6时.①求点P的坐标;②求△ABP的面积S△ABP和△ACP的面积S△ACP.
(2)当a<-
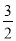 时,随着a的值变化,猜想
时,随着a的值变化,猜想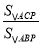 的值是否变化,若变化说明理由,若不变,求出结果.
的值是否变化,若变化说明理由,若不变,求出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b为相反数,c、d互为倒数
(1)a+b=____,cd=____.
(2)若x=3(a﹣1)﹣(a﹣2b),y=c2d﹣(c﹣2),
①求x、y的值.
②计算﹣xy﹣x+y﹣xy.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨)
水价(元/吨)
第一级 20吨以下(含20吨)
1.6
第二级 20吨﹣30吨(含30吨)
2.4
第三级 30吨以上
3.2
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
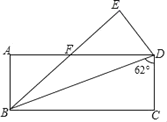
A. 62°B. 56°C. 31°D. 28°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在今年“五一”小长假期间,某学校团委要求学生参加一项社会调查活动,八年级学生小明想了解他所居住的小区500户居民的家庭收入情况,从中随机调查了本小区一定数量居民家庭的收入情况(收入取整数,单位:元),并将调查的数据绘制成如下直方图和扇形图,根据图中提供的信息,解答下列问题:
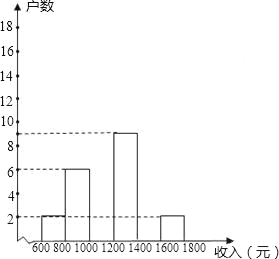
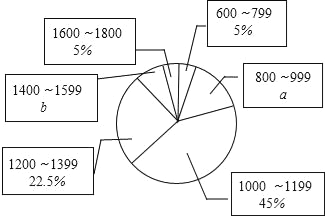
(1)这次共调查了 个家庭的收入,a= ,b= ;
(2)补全频数分布直方图,样本的中位数落在第 个小组;
(3)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
(4)在第1组和第5组的家庭中,随机抽取2户家庭,求这两户家庭人均月收入差距不超过200元的概率.
相关试题

