【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)8,4,4![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)先确定出OA=4,OC=8,进而得出AB=8,BC=4,利用勾股定理即可得出AC;
(2)A.①利用折叠的性质得出BD=8﹣AD,最后用勾股定理即可得出结论;
②分三种情况利用方程的思想即可得出结论;
B.①利用折叠的性质得出AE,利用勾股定理即可得出结论;
②先判断出∠APC=90°,再分情况讨论计算即可.
试题解析:解:(1)∵一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,∴A(4,0),C(0,8),∴OA=4,OC=8.∵AB⊥x轴,CB⊥y轴,∠AOC=90°,∴四边形OABC是矩形,∴AB=OC=8,BC=OA=4.在Rt△ABC中,根据勾股定理得,AC=![]() =4
=4![]() .故答案为:8,4,4
.故答案为:8,4,4![]() ;
;
(2)选A.①由(1)知,BC=4,AB=8,由折叠知,CD=AD.在Rt△BCD中,BD=AB﹣AD=8﹣AD,根据勾股定理得,CD2=BC2+BD2,即:AD2=16+(8﹣AD)2,∴AD=5;
②由①知,D(4,5),设P(0,y).∵A(4,0),∴AP2=16+y2,DP2=16+(y﹣5)2.∵△APD为等腰三角形,∴分三种情况讨论:
Ⅰ、AP=AD,∴16+y2=25,∴y=±3,∴P(0,3)或(0,﹣3);
Ⅱ、AP=DP,∴16+y2=16+(y﹣5)2,∴y=![]() ,∴P(0,
,∴P(0,![]() );
);
Ⅲ、AD=DP,25=16+(y﹣5)2,∴y=2或8,∴P(0,2)或(0,8).
综上所述:P(0,3)或(0,﹣3)或P(0,![]() )或P(0,2)或(0,8).
)或P(0,2)或(0,8).
选B.①由A①知,AD=5,由折叠知,AE=![]() AC=2
AC=2![]() ,DE⊥AC于E.在Rt△ADE中,DE=
,DE⊥AC于E.在Rt△ADE中,DE=![]() =
=![]() ;
;
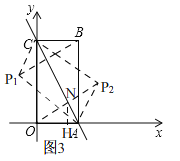
②∵以点A,P,C为顶点的三角形与△ABC全等,∴△APC≌△ABC,或△CPA≌△ABC,∴∠APC=∠ABC=90°.∵四边形OABC是矩形,∴△ACO≌△CAB,此时,符合条件,点P和点O重合,即:P(0,0);
如图3,过点O作ON⊥AC于N,易证,△AON∽△ACO,∴![]() ,∴
,∴![]() ,∴AN=
,∴AN=![]() ,过点N作NH⊥OA,∴NH∥OA,∴△ANH∽△ACO,∴
,过点N作NH⊥OA,∴NH∥OA,∴△ANH∽△ACO,∴![]() ,∴
,∴![]() ,∴NH=
,∴NH=![]() ,AH=
,AH=![]() ,∴OH=
,∴OH=![]() ,∴N(
,∴N(![]() ),而点P2与点O关于AC对称,∴P2(
),而点P2与点O关于AC对称,∴P2(![]() ),同理:点B关于AC的对称点P1,同上的方法得,P1(﹣
),同理:点B关于AC的对称点P1,同上的方法得,P1(﹣![]() ).
).
综上所述:满足条件的点P的坐标为:(0,0),(![]() ),(﹣
),(﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )

A. (
 ,
,  ) B. (
) B. (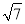 ,11) C. (2,2
,11) C. (2,2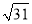 ) D. (
) D. ( ,
, 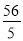 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m,n(m<n),则下列判断正确的是( )
A. m<n<x1<x2 B. m<x1<x2<n C. x1+x2>m+n D. b2-4ac≥0
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两人进行跑步训练,他们所跑的路程y(米)与时间x(秒)之间的关系如图所示,则下列说法错误的是( )

A. 离终点40米处,乙追上甲B. 甲比乙迟3秒到终点
C. 甲跑步的速度是5米/秒D. 乙跑步的速度是
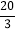 米/秒
米/秒 -
科目: 来源: 题型:
查看答案和解析>>【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8
+1
﹣1.2
0
﹣0.7
+0.6
﹣0.4
﹣0.1
问:(1)这个小组男生的达标率为多少?(达标率=
 )
)(2)这个小组男生的平均成绩是多少秒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在运动会径赛中,甲、乙同时起跑,刚跑出200m,甲不慎摔倒,他又迅速地爬起来继续投入比赛,若他们所跑的路程y(m)与比赛时间x(s)的关系如图,有下列说法:①他们进行的是800m比赛;②乙全程的平均速度为6.4m/s;③甲摔倒之前,乙的速度快;④甲再次投入比赛后的平均速度为7.5m/s;⑤甲再次投入比赛后在距离终点300米时追上了乙.其中正确的个数有( )
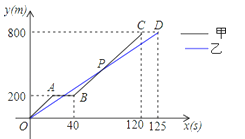
A.2个B.3个C.4个D.5个
相关试题

