【题目】已知:△DEC的一个顶点D在△ABC内部,且∠CAD+∠CBD=90°.
(1)如图1,若△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,连接BE,求证:△ADC∽△BEC.
(2)如图2,若∠ABC=∠DEC=90°, ![]() =
= ![]() =n,BD=1,AD=2,CD=3,求n的值;
=n,BD=1,AD=2,CD=3,求n的值;
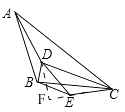
(3)如图3,若AB=BC,DE=EC,且∠ABC=∠DEC=135°,BD=a,AD=b,CD=c,请直接写出a、b、c三者满足的等量关系.
参考答案:
【答案】
(1)
证明: ∵△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,
∴△ABC∽△DEC,
∴ ![]() ,∠ACB=∠DCE,
,∠ACB=∠DCE,
∴∠ACD=∠BCE,
∵ ![]() ,
,
∴△ACD∽△BCE
(2)
解:在Rt△ABC中,AC= ![]() =
= ![]() BC,
BC,
同理:CD= ![]() EC,
EC,
∵∠ABC=∠DEC=90°,
∵ ![]() =
= ![]() ,
,
∴ ![]()
∴△ABC∽△DEC,
∴ ![]() =
= ![]() ,∠ACB=∠DCE,
,∠ACB=∠DCE,
∴∠ACD=∠BCE,
∵ ![]() ,
,
∴△ACD∽△BCE,
∴ ![]() =
= ![]() ,
,
∴AD= ![]() BE,
BE,
∵AD=2,
∴BE= ![]() ,
,
在Rt△CDE中,CD2=DE2+CE2=(n2+1)CE2=9,
∴CE2= ![]()
∴DE2=n2CE2=n2× ![]() =
= ![]() ,
,
∵△ACD∽△BCE,
∴∠CAD=∠CBE,∵∠CAD+∠CBD=90°,
∴∠DBE=∠CBE+∠CBE=90°,
在Rt△BDE中,DE2=BD2+BE2=1+ ![]() ,
,
∴ ![]() =1+
=1+ ![]() ,
,
∴n=﹣ ![]() (舍)或n=
(舍)或n= ![]()
(3)
解:c2﹣b2=(2+ ![]() )a2,
)a2,
理由:如图,∵AB=BC,DE=EC,
∴ ![]() ,
,
∵∠ABC=∠DEC,
∴△ABC∽△DEC,
∴ ![]() ,
,
∵AB=BC,DE=EC,且∠ABC=∠DEC=135°,
∴∠ACB=∠DCE=22.5°,
∴∠ACD=∠BCE,
∵ ![]() ,
,
∴△ACD∽△BCE,
∴ ![]() ,
,
∴ ![]() ,
,
过点D作DF⊥CE交CE的延长线于F,
∵∠DEC=135°,
∴∠DEF=45°,
设DF=x,
∴EF=x,DE= ![]() x,
x,
∵EC=DE= ![]() x,
x,
∴CF=EF+EC=( ![]() +1)x,
+1)x,
在Rt△CDF中,CF2+DF2=CD2,
∴[( ![]() +1)x]2+x2=c2,
+1)x]2+x2=c2,
∴x2= ![]() ,
,
∴DE2=2x2= ![]() ,
,
∴BE2= ![]() =
= ![]() ×
× ![]() =
= ![]() ,
,
∵△ACD∽△BCE,
∴∠CAD=∠CBE,
∵∠CAD+∠CBD=90°,
∴∠DBE=∠CBE+∠CBE=90°,
在Rt△BDE中,DE2=BD2+BE2,
∴ ![]() =a2+
=a2+ ![]() ,
,
∴c2﹣b2=(2+ ![]() )a2.
)a2.
【解析】(1)先判断出△ABC∽△DEC,得出 ![]() ,即可得出结论;(2)先求出AC=
,即可得出结论;(2)先求出AC= ![]() BC,同理:CD=
BC,同理:CD= ![]() EC,再判断出△ABC∽△DEC,得出比例式,继而判断出△ACD∽△BCE,即可得出AD=
EC,再判断出△ABC∽△DEC,得出比例式,继而判断出△ACD∽△BCE,即可得出AD= ![]() BE,BE=
BE,BE= ![]() ,再利用勾股定理得出DE2=
,再利用勾股定理得出DE2= ![]() 再判断出∠DBE=90°,再用勾股定理得出DE的平方,用DE的平方建立方程求解即可;(3)同(2)的方法
再判断出∠DBE=90°,再用勾股定理得出DE的平方,用DE的平方建立方程求解即可;(3)同(2)的方法 ![]() ,再构造直角三角形,利用勾股定理即可得出结论.
,再构造直角三角形,利用勾股定理即可得出结论.
-
科目: 来源: 题型:
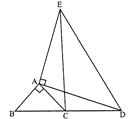
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知
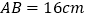 ,
,
⑴若
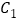 是
是 的中点,则
的中点,则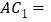 _____
_____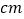 ;
;⑵若
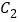 是
是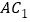 的中点,则
的中点,则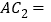 _____
_____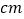 ;
;⑶若
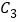 是
是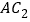 的中点,则
的中点,则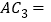 ____
____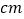 ;
;⑷以此类推,若C100是AC99的中点,则AC100=____
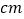 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】AB、AC是同一条直线上的两条线段,M在AB上,且AM=
 AB,N在AC上,且AN=
AB,N在AC上,且AN= AC,线段BC和MN的大小有什么关系?请说明理由.
AC,线段BC和MN的大小有什么关系?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)直线y=kx+4经过点(1,2),求不等式kx+4≥0的解集.
(2)x取哪些正整数时,不等式 x+3>6 与 2x-1<10 都成立?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.

(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y=kx与反比例函数y=
 的图象不可能是( )
的图象不可能是( )
A.
B.
C.
D.
相关试题

