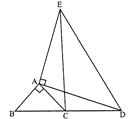
【题目】如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.
参考答案:
【答案】证明:∵△ABC和△ADE都是等腰直角三角形
∴AD=AE AB=AC
又∵∠EAC=90°+∠CAD, ∠DAB=90°+∠CAD
∴∠DAB=∠EAC
在△ADB和△AEC中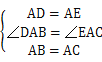
∴△ADB≌△AEC(SAS)
【解析】试题分析:求出AD=AE,AB=AC,∠DAB=∠EAC,根据SAS证出△ADB≌△AEC即可.
证明:∵△ABC和△ADE都是等腰直角三角形
∴AD=AE,AB=AC,
又∵∠EAC=90°+∠CAD,∠DAB=90°+∠CAD,
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
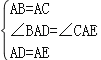
∴△ADB≌△AEC(SAS),
∴BD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=
 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.
下面是他的探究过程,请将(1)、(2)、(3)补充完整:
将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1> ;
;
当x<0时,原不等式可以转化为x2+4x﹣1< ;
;
(1)构造函数,画出图象 设y3=x2+4x﹣1,y4= ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(2)确定两个函数图象公共点的横坐标 观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为;
(3)借助图象,写出解集 结合讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小力在电脑上设计了一个有理数运算程序:输入a,加※键,再输入b,得到运算a※b=a2-b2-[2(a-1)-
 ]÷(a-b).
]÷(a-b).(1)求(-2)※
 的值;
的值;(2)小华在运用此程序计算时,屏幕显示“该程序无法操作”,你猜小华在输入数据时,可能出现什么情况?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为1米,一个人从入口点A沿着道路中央走到中点B,他共走了( )

A. 55米 B. 55.5米 C. 56米 D. 56.5米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知
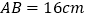 ,
,
⑴若
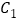 是
是 的中点,则
的中点,则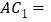 _____
_____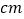 ;
;⑵若
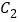 是
是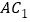 的中点,则
的中点,则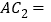 _____
_____ ;
;⑶若
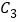 是
是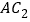 的中点,则
的中点,则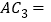 ____
____ ;
;⑷以此类推,若C100是AC99的中点,则AC100=____
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】AB、AC是同一条直线上的两条线段,M在AB上,且AM=
 AB,N在AC上,且AN=
AB,N在AC上,且AN= AC,线段BC和MN的大小有什么关系?请说明理由.
AC,线段BC和MN的大小有什么关系?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△DEC的一个顶点D在△ABC内部,且∠CAD+∠CBD=90°.
(1)如图1,若△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,连接BE,求证:△ADC∽△BEC.
(2)如图2,若∠ABC=∠DEC=90°, =
=  =n,BD=1,AD=2,CD=3,求n的值;
=n,BD=1,AD=2,CD=3,求n的值;
(3)如图3,若AB=BC,DE=EC,且∠ABC=∠DEC=135°,BD=a,AD=b,CD=c,请直接写出a、b、c三者满足的等量关系.
相关试题

