【题目】AB、AC是同一条直线上的两条线段,M在AB上,且AM=![]() AB,N在AC上,且AN=
AB,N在AC上,且AN=![]() AC,线段BC和MN的大小有什么关系?请说明理由.
AC,线段BC和MN的大小有什么关系?请说明理由.
参考答案:
【答案】BC=3MN,理由见解析.
【解析】由于AB、AC两线段的位置关系不明确,所以应考虑B、C两点的位置,可能在A点同侧也可能在A点异侧,接下来利用线段之间的和倍关系即可求解.
详解:BC=3MN.分三种情况:
(1)如图所示:
![]()
∵AM=![]() AB,AN=
AB,AN=![]() AC,
AC,
∴MN=ANAM=![]() (ACAB),
(ACAB),
∵MN=![]() ACAB),BC=AC-AB,
ACAB),BC=AC-AB,
∴ BC=3MN;
(2)如图所示:
![]()
同理可得到BC=3MN;
(3)如图所示:
![]()
∵AM=![]() AB,AN=
AB,AN=![]() AC,AB+AC=BC,
AC,AB+AC=BC,
∴BC=3MN.
综上所述,无论B、C在点A的同侧还是异侧都有BC=3MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为1米,一个人从入口点A沿着道路中央走到中点B,他共走了( )

A. 55米 B. 55.5米 C. 56米 D. 56.5米
-
科目: 来源: 题型:
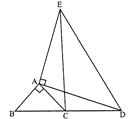
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知
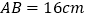 ,
,
⑴若
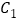 是
是 的中点,则
的中点,则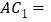 _____
_____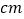 ;
;⑵若
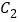 是
是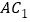 的中点,则
的中点,则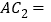 _____
_____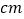 ;
;⑶若
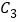 是
是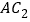 的中点,则
的中点,则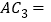 ____
____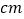 ;
;⑷以此类推,若C100是AC99的中点,则AC100=____
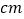 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△DEC的一个顶点D在△ABC内部,且∠CAD+∠CBD=90°.
(1)如图1,若△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,连接BE,求证:△ADC∽△BEC.
(2)如图2,若∠ABC=∠DEC=90°, =
=  =n,BD=1,AD=2,CD=3,求n的值;
=n,BD=1,AD=2,CD=3,求n的值;
(3)如图3,若AB=BC,DE=EC,且∠ABC=∠DEC=135°,BD=a,AD=b,CD=c,请直接写出a、b、c三者满足的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)直线y=kx+4经过点(1,2),求不等式kx+4≥0的解集.
(2)x取哪些正整数时,不等式 x+3>6 与 2x-1<10 都成立?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.

(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
相关试题

