【题目】计算题
(1)解不等式组:  .
.
(2)化简:(x﹣ ![]() )÷
)÷ ![]() .
.
参考答案:
【答案】
(1)解:由3(x﹣1)<5x+1
可得:x>﹣2
由 ![]() ≥2x﹣4
≥2x﹣4
可得:x≤ ![]()
∴不等式组的解集为:﹣2<x≤ ![]()
(2)解:原式= ![]() ×
× ![]()
= ![]()
= ![]()
【解析】(1)解不等式1得x>﹣2,解不等式2得x≤ ![]() ,然后根据大小小大中间找得出解集;
,然后根据大小小大中间找得出解集;
(2)把整式看成分母为一,然后通分算减法,然后再算除法,分子分母能分解因式的必须分解因式,然后约分化简到最简形式即可。
【考点精析】通过灵活运用分式的混合运算和一元一次不等式组的解法,掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )即可以解答此题.
-
科目: 来源: 题型:
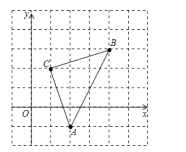
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
(1)写出点A、B的坐标:A(_____,_____)、B(_____,_____);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′、B′、C′三点坐标;
(3)求△ABC的面积。
-
科目: 来源: 题型:
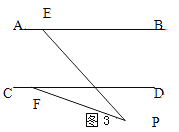
查看答案和解析>>【题目】如图,直线AB∥CD,点P在两平行直线之间,点E在AB上,点F在CD上,连接PE、PF。
(1)∠PEB、∠PFD、∠EPF满足什么数量关系?请说明理由。
(2)如果点P在两平行线外时,试探究∠PEB、∠PFD、∠EPF之间的数量关系。(不需说明理由)
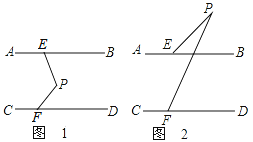
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
A.
 B.
B.  C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】青岛是全车著名的海滨旅游城市,有丰富的旅游产品.某校九年级(1)班的同学就部分旅游产品的喜爱情况对游客随机调查,要求游客在列举的旅游产品中选出喜爱的产品,且只能选一项.以下是同学们根据游客选择整理的不完整的统计图(图①为旅游产品喜爱情况条形统计图,图②为旅游产品喜爱情况扇形统计图):
根据以上信息完成下列问题:
(1)随机调查的游客有多少人;在扇形统计图中,A部分所占的圆心角是多少度.
(2)请将条形统计图①补充完整.
(3)请根据调查结果估计在3000名游客中喜爱大泽山葡萄的约有多少人. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′(点B的对应点是点B',点C的对应点是点C'),连接BB′,若AC′∥BB′,则∠C'AB′的度数为( )

A. 15°B. 30°C. 45°D. 60°
相关试题

