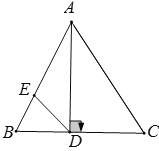
【题目】如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.
参考答案:
【答案】(1)34°(2)109°
【解析】
(1)在Rt△BAD和Rt△BAD中,根据直角三角形的两个锐角互余分别求解即可得;
(2)由DE平分∠ADB,AD⊥BC求得∠BDE=45°,再根据三角形外角的性质求解即可.
(1)∵AD⊥BC,
∴在Rt△BAD中,∠BAD+∠B=90°,
又∵∠B=64°,∴∠BAD=26°;
∴在Rt△BAD中,∠DAC+∠C=90°,
又∵∠C=56°,∴∠DAC=34°;
(2)∵AD⊥BC,DE平分∠ADB,∴∠BDE=45°,
在△BED中,∠B=64°,∴∠B+∠BDE=109°,
∵∠AED=∠B+∠BDE,
∴∠AED=109°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
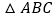 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点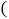 点D不与B,C重合
点D不与B,C重合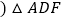 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.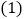 如图1,求证:
如图1,求证: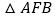 ≌
≌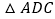 ;
; 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由; 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )

A.56° B.66° C.76° D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BED中作BD边上的高,垂足为F;
(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书
书本类别
A类
B类
进价(单位:元)
18
12
备注
1、用不超过16800元购进A、B两类图书共1000本;
2、A类图书不少于600本;
…
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润? -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.

-
科目: 来源: 题型:
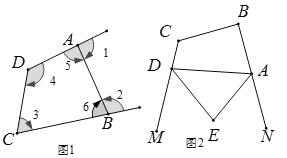
查看答案和解析>>【题目】(1)如图1,试探究其中∠1,∠2与∠3,∠4之间的关系,并证明.
(2)用(1)中的结论解决下列问题:如图2,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
相关试题

