【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.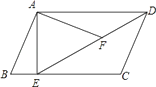
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD= ![]() ,AE=3,求AF的长.
,AE=3,求AF的长.
参考答案:
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°;
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC
(2)解:∵CD=AB=4,AE⊥BC,
∴AE⊥AD; 在Rt△ADE中,DE= ![]() ,
,
∵△ADF∽△DEC,
∴ ![]() ;
;
∴ ![]() ,
,
解得AF= ![]()
【解析】(1)根据平行四边形的性质证出AD∥BC,AB∥CD,结合已知∠AFE=∠B.得出∠ADF=∠CED,∠AFD=∠C再根据两组角对应相等的两个三角形相似证得结论。
(2)根据平行四边形的性质及已知AE⊥BC,证明△ADE是直角三角形,利用勾股定理求出DE的长,再根据相似三角形的性质(△ADF∽△DEC)。得对应线段成比例,建立方程求出AF的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
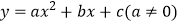 的对称轴为直线
的对称轴为直线 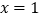 ,与
,与 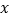 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: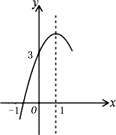
①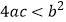 ;② 方程
;② 方程 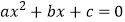 的两个根是
的两个根是 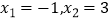 ;③
;③  ;④当
;④当  时,
时, 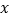 的取值范围是
的取值范围是 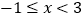 ;⑤ 当
;⑤ 当  时,
时, 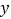 随
随 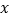 增大而增大;其中结论正确有.
增大而增大;其中结论正确有. -
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,重百超市推出了甲、乙、丙、丁四种礼品套餐组合:甲套餐每袋装有15个A礼盒,10个B礼盒,10个C礼盒;乙套餐每袋装有5个A礼盒,7个B礼盒,6个C礼盒;丙套餐每袋装有7个A礼盒,8个B礼盒,9个C礼盒;丁套餐每袋装有3个A礼盒,4个B礼盒,4个C礼盒,若一个甲套餐售价1800元,利润率为
 ,一个乙和一个丙套餐一共成本和为1830元,且一个A礼盒的利润率为
,一个乙和一个丙套餐一共成本和为1830元,且一个A礼盒的利润率为 ,问一个丁套餐的利润率为______
,问一个丁套餐的利润率为______ 利润率
利润率
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
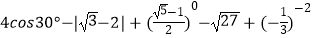 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在山脚的C处测得山顶A的仰角为
 ,沿着坡角为
,沿着坡角为  的斜坡前进400米到D处(即
的斜坡前进400米到D处(即  ,
,  米),测得山顶A的仰角为
米),测得山顶A的仰角为  ,求山的高度AB.
,求山的高度AB.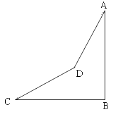
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).
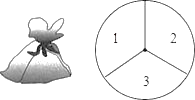
(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:
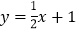 与x轴交于点C,两直线
与x轴交于点C,两直线 ,
, 相交于点B.
相交于点B.(1)求直线
 的解析式和点B的坐标;
的解析式和点B的坐标;(2)求△ABC的面积.

相关试题

