【题目】如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.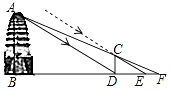
参考答案:
【答案】解:由题意得,∠ABD=∠CDE=90°,∠ADB=∠CED,
∴△CDE∽△ABD,
∴ ![]() =
= ![]() ,
,
∵∠F=∠F,
∴△CDF∽△ABF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴BD=60,
∴ ![]() =
= ![]() ,
,
∴AB=43,
答:小雁塔的高度AB是43米
【解析】利用太阳光线是平行的,可得△CDF∽△ABF,对应边成比例可列出方程,求出BD,进而求出AB.
【考点精析】本题主要考查了相似三角形的应用和平行投影的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解;太阳光线可以看成是平行光线,平行光线所形成的投影称为平行投影;作物体的平行投影:由于平行投影的光线是平行的,而物体的顶端与影子的顶端确定的直线就是光线,故根据另一物体的顶端可作出其影子才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
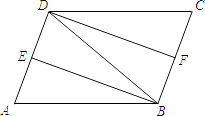
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店购进一批甲、乙两种款型时尚
 恤衫,甲种款型共用了7800元,乙种款型共用了6400元.甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
恤衫,甲种款型共用了7800元,乙种款型共用了6400元.甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.(1)甲、乙两种款型的
 恤衫各购进多少件?
恤衫各购进多少件?(2)商店进价提高50%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批
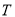 恤衫商店共获利多少元?
恤衫商店共获利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, 分别为边
分别为边 的中点,
的中点, 是对角线,过点
是对角线,过点 作
作 交
交 的延长线于点
的延长线于点 .
.(1)求证:
 .
.(2)若
 ,
,①求证:四边形
 是菱形.
是菱形.②当
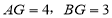 时,求四边形
时,求四边形 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“湘一四边形”.
(1)已知:如图1,四边形
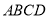 是“湘一四边形”,
是“湘一四边形”,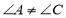 ,
,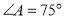 ,
,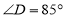 .则
.则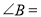 ,
, 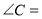 ,若
,若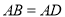 ,
,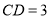 ,则
,则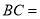 (直接写答案)
(直接写答案)(2)已知:在“湘一四边形”
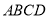 中,
中,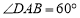 ,
,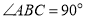 ,
,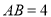 ,
,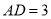 .求对角线
.求对角线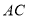 的长(请画图求解),
的长(请画图求解),(3)如图(2)所示,在四边形
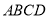 中,若
中,若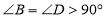 ,当
,当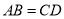 时,此时四边形
时,此时四边形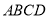 是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.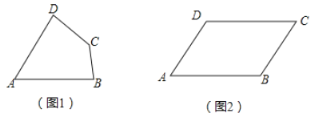
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一枚质地均匀的正四面体骰子,它的四个面上分别标有数字0,1,2,3,如图2,正方形ABCD的四个顶点处均有一个圈.课间,李丽和王萍利用它们玩跳圈游戏,玩法如下:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形ABCD的边顺时针分钟连续跳几个边长.
例如:若从圈A起跳,第一掷得的数字为2,便沿正方形的边顺时针连续跳2个边长,落到圈C,第二次掷得的数字为3,便从圈C开始,沿正方形的边顺时针连续跳3个边长,落到圈B,….
设她们从圈A起跳.
(1)若李丽随机掷这枚骰子一次,求她跳回圈A的概率;
(2)若王萍随机掷这枚骰子两次,请用列表法或画树状图求她最后跳回圈A的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠CBF=
 ∠CAB.
∠CAB.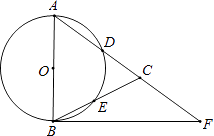
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=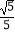 ,求BC和BF的长.
,求BC和BF的长.
相关试题

