搜索
【题目】下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形由3颗棋子，第②个图形一共有9颗棋子，第③个图形一共有18个棋子，…，则第⑥个图形中棋子的颗数为（ ）
A.63B.84C.108D.152
参考答案：
【答案】A
【解析】
根据第①个图形的棋子数是3＝3×1，第②个图形的棋子数是9＝3×（1＋2），第③个图形的棋子数是18＝3×（1＋2＋3），…，可得第n个图形的棋子数是3×（1＋2＋…＋n），据此求出第⑥个图形中棋子的颗数为多少即可．
∵第①个图形的棋子数是3＝3×1，
第②个图形的棋子数是9＝3×（1＋2），
第③个图形的棋子数是18＝3×（1＋2＋3），
…，
∴第n个图形的棋子数是3×（1＋2＋…＋n），
∴第⑥个图形中棋子的颗数为：
3×（1＋2＋…＋6）
＝3×21
＝63．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，如图所示的函数图象是由函数y=（x﹣1）2+1（x≥0）的图象C1和图象C2组成中心对称图形，对称中心为点（0，2）．已知不重合的两点A、B分别在图象C1和C2上，点A、B的横坐标分别为a、b，且a+b=0．当b＜x≤a时该函数的最大值和最小值均与a、b的值无关，则a的取值范围为_____．
-
科目： 来源： 题型：
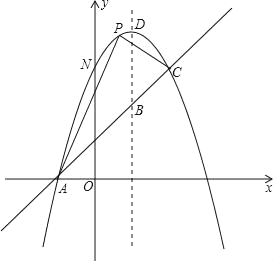
查看答案和解析>>【题目】如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0）、C（2，3）两点，与y轴交于点N，其顶点为D．
（1）求抛物线及直线AC的函数关系式；
（2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；
（3）设点M（3，n），求使MN+MD取最小值时n的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】王师傅承包了一片池塘养水产品，他用总长为88m的围网围成如图所示的5个区域，其中②③④⑤四个区域面积相等．设AH=xm，整个矩形区域的面积为ym2．
（1）求y与x之间的函数关系式，并注明自变量x的取值范围；
（2）当x为何值时，y取最大值？最大值是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】胖娃、猴子两人在1800米长的直线道路上跑步，胖娃、猴子两人同起点、同方向出发，并分别以不同的速度匀速前进.已知，胖娃出发30秒后，猴子出发，猴子到终点后立即返回，并以原来的速度前进，最后与胖娃相遇，此时跑步结束. 如图，
（米）表示胖娃、猴子两人之间的距离，x（秒）表示胖娃出发的时间，图中折线及数据表示整个跑步过程中y与x函数关系.那么，猴子到终点后_______秒与胖娃相遇.
-
科目： 来源： 题型：
查看答案和解析>>【题目】重庆电视台组织了一次学生夏令营活动，有小学生、初中生、高中生和大学生参加，共200人，各类学生人数比例见扇形统计图．
（1）参加这次夏令营活动的初中生共有__________人.
（2）活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款. 结果小学生每人捐款5元，初中生每人捐款10元，高中生每人捐款15元，大学生每人捐款20元，把每个学生的捐款数（以元为单位）一一记录下来，则在这组数据中，中位数是 元，求出平均每人捐款多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，直线l1:y=2x+3与直线l2:y=kx+b的交点A在y轴上，直线l3:y=x与直线l1相交于点B与直线l2相交于点C（1，1）.
（1）求直线l2的解析式和B点的坐标;
（2）求△ABC的面积.
相关试题
