【题目】已知函数![]() ,
,
(1)通过配方,写出其对称轴,顶点坐标;
(2)分别求出其与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
(3)画出函数的大致图象,结合图象说明,当![]() 取何值时,
取何值时,![]() ?
?
参考答案:
【答案】(1)对称轴为直线![]() ,顶点坐标为
,顶点坐标为![]() ;(2)与
;(2)与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,![]() ,与
,与![]() 轴的交点坐标为
轴的交点坐标为![]() ;(3)图象详见解析,当
;(3)图象详见解析,当![]() 时,
时,![]() .
.
【解析】
(1)先提取二次项系数3,然后利用完全平方公式配方即可,再根据二次项系数写出开口方向,然后写出对称轴与顶点坐标;
(2)令y=0,解关于x的一元二次方程求出与x轴的交点坐标,令x=0求出于y轴的交点坐标;
(3)根据二次函数的对称性,先确定出对称轴,然后作出大致图象即可.
解:(1)![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,
,
∴抛物线开口方向向上,
对称轴为直线![]() ,
,
顶点坐标为![]() ;
;
(2)令![]() ,则
,则![]() ,
,
解得![]() ,
,![]() ,
,
所以,与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
所以,与![]() 轴的交点坐标为
轴的交点坐标为![]() ;(3)图象如图所示:
;(3)图象如图所示:
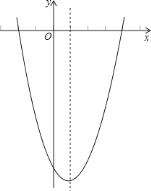
当![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,Rt△ABC和Rt△ABD中,∠ACB=∠ADB=90°,E为AB中点.
(1)若两个直角三角形的直角顶点在AB的异侧(如图1),连接CD,取CD中点F,连接EF、DE、CE,则DE与CE数量关系为 ,EF与CD位置关系为 ;
(2)若两个直角三角形的直角顶点在AB的同侧(如图2),连接CD、DE、CE.
①若∠CAB=25°,∠DBA=35°,判断△DEC的形状,并说明理由;
②若∠CAB+∠DBA=
 ,当
,当 为多少度时,△DEC为等腰直角三角形,并说明理由.
为多少度时,△DEC为等腰直角三角形,并说明理由.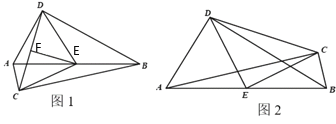
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.
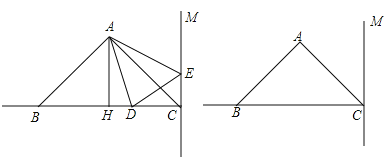
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,图形的运动只改变图形的位置,不改变图形的形状、大小,运动前后的两个图形全等,翻折就是这样.如图1,将△ABC沿AD翻折,使点C落在AB边上的点C'处,则△ADC≌△ADC'.
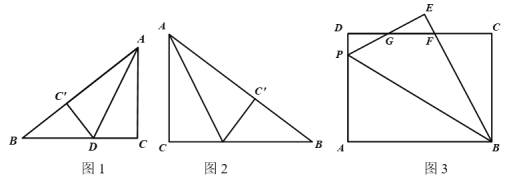
尝试解决:(1)如图2,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD翻折,使点C落在AB边上的点C'处,求CD的长.
(2)如图3,在长方形ABCD中,AB=8,AD=6,点P在边AD上,连接BP,将△ABP沿BP翻折,使点A落在点E处,PE、BE分别与CD交于点G、F,且DG=EG.
①求证:PE=DF;
②求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一轮船在
 处测得灯塔
处测得灯塔 在正北方向,灯塔
在正北方向,灯塔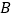 在南偏东
在南偏东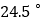 方向,轮船向正东航行了
方向,轮船向正东航行了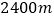 ,到达
,到达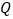 处,测得
处,测得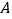 位于北偏西
位于北偏西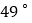 方向,
方向,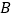 位于南偏西
位于南偏西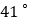 方向.
方向. 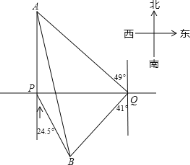
(1)线段
 与
与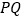 是否相等?请说明理由;
是否相等?请说明理由;(2)求
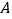 、
、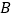 间的距离(参考数据
间的距离(参考数据 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个外角为100°,则这个等腰三角形的顶角为________;等腰三角形一腰上的高与腰的夹角为36°,则该等腰三角形的顶角为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
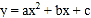 的图象开口向上,图象经过点
的图象开口向上,图象经过点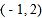 和
和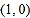 ,且与
,且与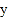 轴相交于负半轴.
轴相交于负半轴.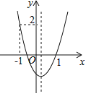
第
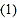 问:给出四个结论:①
问:给出四个结论:①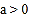 ;②
;②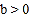 ;③
;③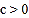 ;④
;④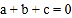 .写出其中正确结论的序号(答对得
.写出其中正确结论的序号(答对得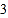 分,少选、错选均不得分)
分,少选、错选均不得分)第
 问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
相关试题

