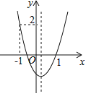
【题目】如图,二次函数![]() 的图象开口向上,图象经过点
的图象开口向上,图象经过点![]() 和
和![]() ,且与
,且与![]() 轴相交于负半轴.
轴相交于负半轴.
第![]() 问:给出四个结论:①
问:给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .写出其中正确结论的序号(答对得
.写出其中正确结论的序号(答对得![]() 分,少选、错选均不得分)
分,少选、错选均不得分)
第 ![]() 问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
参考答案:
【答案】(1)正确的序号为①④;(2)正确的序号为②③④.
【解析】
(1)根据抛物线开口向上对①进行判断;根据抛物线对称轴x=-![]() 在y轴右侧对②进行判断;根据抛物线与y轴的交点在x轴下方对③进行判断;根据x=1时,y=0对④进行判断;
在y轴右侧对②进行判断;根据抛物线与y轴的交点在x轴下方对③进行判断;根据x=1时,y=0对④进行判断;
(2)有(1)得到a>0,b<0,c<0,则可对①进行判断;根据0<-![]() <1可对②进行判断;把点(-1,2)和(1,0)代入解析式得a﹣b+c=2,a+b+c=0,整理有a+c=1,则可对③进行判断;根据a=1-c,c<0可对④进行判断.
<1可对②进行判断;把点(-1,2)和(1,0)代入解析式得a﹣b+c=2,a+b+c=0,整理有a+c=1,则可对③进行判断;根据a=1-c,c<0可对④进行判断.
(1)①由抛物线的开口方向向上可推出a>0,正确;
②因为对称轴在y轴右侧,对称轴为x=![]() >0.
>0.
又∵a>0,∴b<0,错误;
③由抛物线与y轴的交点在y轴的负半轴上,∴c<0,错误;
④由图象可知:当x=1时y=0,∴a+b+c=0,正确.
故(1)中,正确结论的序号是①④.
(2)①∵a>0,b<0,c<0,∴abc>0,错误;
②由图象可知:对称轴x=![]() >0且对称轴x=
>0且对称轴x=![]() <1,∴2a+b>0,正确;
<1,∴2a+b>0,正确;
③由图象可知:当x=﹣1时y=2,∴a﹣b+c=2,当x=1时y=0,∴a+b+c=0;
a﹣b+c=2与a+b+c=0相加得2a+2c=2,解得:a+c=1,正确;
④∵a+c=1,移项得:a=1﹣c.
又∵c<0,∴a>1,正确.
故(2)中,正确结论的序号是②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, (1)通过配方,写出其对称轴,顶点坐标;
(2)分别求出其与
 轴、
轴、 轴的交点坐标;
轴的交点坐标;(3)画出函数的大致图象,结合图象说明,当
 取何值时,
取何值时, ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】一轮船在
 处测得灯塔
处测得灯塔 在正北方向,灯塔
在正北方向,灯塔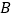 在南偏东
在南偏东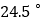 方向,轮船向正东航行了
方向,轮船向正东航行了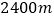 ,到达
,到达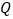 处,测得
处,测得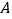 位于北偏西
位于北偏西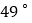 方向,
方向,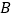 位于南偏西
位于南偏西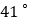 方向.
方向. 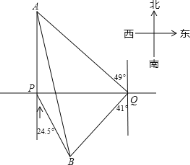
(1)线段
 与
与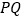 是否相等?请说明理由;
是否相等?请说明理由;(2)求
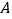 、
、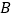 间的距离(参考数据
间的距离(参考数据 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个外角为100°,则这个等腰三角形的顶角为________;等腰三角形一腰上的高与腰的夹角为36°,则该等腰三角形的顶角为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某童装店在服装销售中发现:进货价每件60元,销售价每件100元的某童装每天可售出20件
 为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利
为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利 经调查发现:如果每件童装降价1元,那么每天就可多售出2件.
经调查发现:如果每件童装降价1元,那么每天就可多售出2件.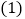 如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?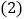 每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元?
每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
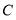 为线段
为线段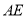 上一动点(不与点
上一动点(不与点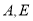 重合),在
重合),在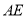 同侧分别作等边三角形
同侧分别作等边三角形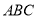 和等边三角形
和等边三角形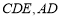 与
与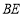 交于点
交于点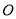 ,
,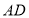 与
与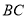 交于点
交于点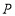 ,
,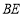 与
与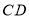 交于点
交于点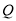 ,连结
,连结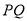 .以下结论:①
.以下结论:①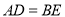 ;②
;②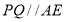 ;③
;③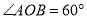 ;④
;④ 是等边三角形,恒成立的是______.
是等边三角形,恒成立的是______.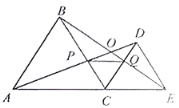
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在
 中,
中,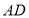 是高,
是高,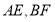 是角平分线,它们相交于点
是角平分线,它们相交于点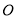 ,
,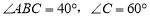 .求
.求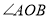 和
和 的度数.
的度数.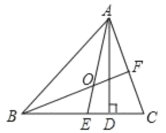
(2)一个多边形的内角和是外角和的3倍,它是几边形?若这个多边形的各个内角都相等,求这个多边形的每个内角的度数.
相关试题

