Question

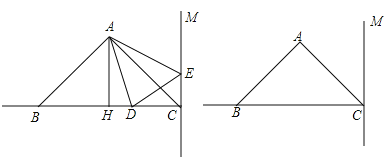
【题目】如图，在△ABC中，已知AB＝AC，∠BAC＝90°，AH是△ABC的高，AH＝4 cm，BC＝8 cm，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒3厘米的速度运动，动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动，连接AD、AE，设运动时间为t（t＞0）秒．

（1）请直接写出CD、CE的长度（用含有t的代数式表示）：CD＝　 　cm，CE＝　 　cm；

（2）当t为多少时，△ABD的面积为12 cm2？

（3）请利用备用图探究，当t为多少时，△ABD≌△ACE？并简要说明理由．

Answer 1

【答案】（1）3t，t；（2）t为s或s；（3）见解析.

【解析】

（1）根据路程=速度×时间，即可得出结果；

（2）首先求出△ABD中BD边上的高，然后根据面积公式列出方程，求出BD的值，分两种情况分别求出t的值即可；

（3）假设△ABD≌△ACE，根据全等三角形的对应边相等得出BD=CE，分别用含t的代数式表示CE和BD，得到关于t的方程，从而求出t的值．

（1）根据题意得：CD＝3tcm，CE＝tcm；

故答案为：3t，t；

（2）∵S△ABDBDAH＝12，AH＝4，

∴AH×BD＝24，

∴BD＝6．

若D在B点右侧，则CD＝BC﹣BD＝2，t；

若D在B点左侧，则CD＝BC+BD＝14，t；

综上所述：当t为s或s时，△ABD的面积为12 cm2；

（3）动点E从点C沿射线CM方向运动2秒或当动点E从点C沿射线CM的反向延长线方向运动4秒时，△ABD≌△ACE．

理由如下：

①当E在射线CM上时，D必在CB上，则需BD＝CE．如图所示，

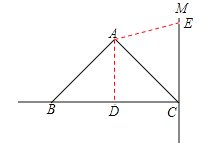
∵CE＝t，BD＝8﹣3t

∴t＝8﹣3t，

∴t＝2，

∵在△ABD和△ACE中，，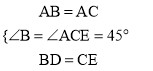

∴△ABD≌△ACE（SAS）．

②当E在CM的反向延长线上时，D必在CB延长线上，则需BD＝CE．如图，

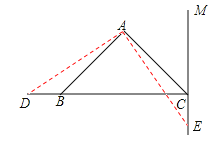
∵CE＝t，BD＝3t﹣8，

∴t＝3t﹣8，

∴t＝4，

∵在△ABD和△ACE中，，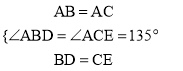

∴△ABD≌△ACE（SAS）．