【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A,B两点,与反比例函数 ![]() 的图象交于C,D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
的图象交于C,D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.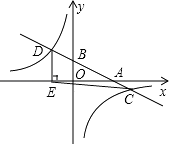
(1)求反比例函数与一次函数的解析式;
(2)求△CDE的面积.
参考答案:
【答案】
(1)解:∵点C(6,﹣1)在反比例y= ![]() 图象上,
图象上, 
∴将x=6,y=﹣1代入反比例解析式得:﹣1= ![]() ,即m=﹣6,
,即m=﹣6,
∴反比例解析式为y=﹣ ![]() ,
,
∵点D在反比例函数图象上,且DE=3,即D纵坐标为3,
将y=3代入反比例解析式得:3=﹣ ![]() ,即x=﹣2,
,即x=﹣2,
∴点D坐标为(﹣2,3),
设直线解析式为y=kx+b,将C与D坐标代入得: ![]() ,
,
解得: 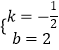 ,
,
∴一次函数解析式为y=﹣ ![]() x+2;
x+2;
(2)解:过C作CH⊥x轴于点H,
∵C(6,﹣1),∴CH=1,
对于一次函数y=﹣ ![]() x+2,令y=0,求得x=4,故A(4,0),
x+2,令y=0,求得x=4,故A(4,0),
由D坐标(﹣2,3),得到E(﹣2,0),
∴AE=OA+OE=6,
∴S△CDE=S△CAE+S△DAE= ![]() ×6×1+
×6×1+ ![]() ×6×3=12.
×6×3=12.
【解析】(1)由点C(6,﹣1)在反比例y=mx 图象上,得到m=﹣6,求出反比例解析式,由点D在反比例函数图象上,且DE=3,即D纵坐标为3,将y=3代入反比例解析式,得到点D坐标为(﹣2,3),设直线解析式为y=kx+b,将C与D坐标代入求出一次函数解析式;(2)由C(6,﹣1),得到CH=1,由一次函数y=﹣![]() x+2求出A(4,0),由D坐标(﹣2,3),得到E(﹣2,0),得到AE=OA+OE,求出S△CDE=S△CAE+S△DAE.
x+2求出A(4,0),由D坐标(﹣2,3),得到E(﹣2,0),得到AE=OA+OE,求出S△CDE=S△CAE+S△DAE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对“学生在学校拿手机影响学习的情况”进行了调查,随机调查了部分学生,对此问题的看法分为三种情况:没有影响、影响不大、影响很大,并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
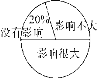
人数统计表如下:
看法
没有影响
影响不大
影响很大
学生人数(人)
20
30
a
(1)统计表中的a= ;
(2)请根据表中的数据,谈谈你的看法(不少于2条)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠FAE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
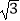 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下叙述正确的有( )
①对顶角相等;②同位角相等;③两直角相等;④邻补角相等;⑤多边形的外角和都相等;⑥三角形的中线把原三角形分成面积相等的两个三角形
A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
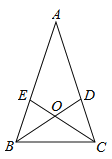
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠ACB的平分线,且交于点O,则图中等腰三角形有________
-
科目: 来源: 题型:
查看答案和解析>>【题目】D,E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB,AC的中点.O是△ABC所在平面上的动点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.

(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图∠1=∠2,∠3=∠4,∠5=∠6,∠1=60°,∠7=20°
(1)试说明AC⊥BD
(2)求∠3及∠5的度数
(3)求四边形ABCD各内角的度数.

相关试题

