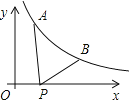
【题目】如图所示,已知A(![]() ,y1),B(2,y2)为反比例函数
,y1),B(2,y2)为反比例函数![]() 图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
参考答案:
【答案】D
【解析】求出AB的坐标,设直线AB的解析式是y=kx+b,把A、B的坐标代入求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,|AP-BP|<AB,延长AB交x轴于P′,当P在P′点时,PA-PB=AB,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
∵把A(![]() ,y1),B(2,y2)代入反比例函数y=
,y1),B(2,y2)代入反比例函数y=![]() 得:y1=2,y2=
得:y1=2,y2=![]() ,
,
∴A(![]() ,2),B(2,
,2),B(2,![]() ),
),
∵在△ABP中,由三角形的三边关系定理得:|AP-BP|<AB,
∴延长AB交x轴于P′,当P在P′点时,PA-PB=AB,
即此时线段AP与线段BP之差达到最大,

设直线AB的解析式是y=kx+b,
把A、B的坐标代入得:
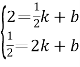 ,
,
解得:k=-1,b=![]() ,
,
∴直线AB的解析式是y=-x+![]() ,
,
当y=0时,x=![]() ,
,
即P(![]() ,0),
,0),
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式
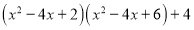 进行因式分解的过程.
进行因式分解的过程.解:设
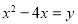 ,
,原式
 (第一步)
(第一步)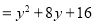 (第二步)
(第二步)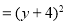 (第三步)
(第三步)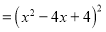 (第四步)
(第四步)回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_____________.
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底__________(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
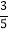 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PAPB的值称为点P关于⊙O的“幂值”
(1)⊙O的半径为6,OP=4.
①如图1,若点P恰为弦AB的中点,则点P关于⊙O的“幂值”为_____;
②判断当弦AB的位置改变时,点P关于⊙O的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P关于⊙0的“幂值”的取值范围;
(2)若⊙O的半径为r,OP=d,请参考(1)的思路,用含r、d的式子表示点P关于⊙O的“幂值”或“幂值”的取值范围_____;
(3)在平面直角坐标系xOy中,C(1,0),⊙C的半径为3,若在直线y=
 x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.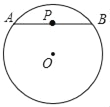
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
 和
和 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥
的图象上,PC⊥ 轴于点C,交
轴于点C,交 的图象于点A,PC⊥
的图象于点A,PC⊥ 轴于点D,交
轴于点D,交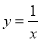 的图象于点B. 当点P在
的图象于点B. 当点P在 的图象上运动时,以下结论:
的图象上运动时,以下结论:①

②
 的值不会发生变化
的值不会发生变化③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(m,6),B(n,1)在反比例函数
 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
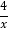 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=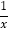 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.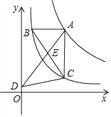
相关试题

