【题目】下面是某同学对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]() ,
,
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() (第四步)
(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_____________.
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底__________(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_____________.
参考答案:
【答案】(1)![]() ;(2)不彻底,
;(2)不彻底,![]()
【解析】
(1)由题意根据题干所给分解因式的过程直接得出答案;
(2)根据题意可知该同学因式分解的结果不彻底,进而再次分解因式得出即可.
解:(1)该同学第二步到第三步运用了因式分解的两数和的完全平方公式;
故选:C;
(2)该同学因式分解的结果不彻底;
原式=(x2-4x+4)2=![]() ;
;
故答案为:不彻底,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点P以每秒2cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,试回答下列问题
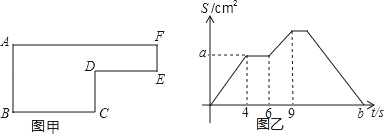
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙中的b是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
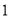 的正方形
的正方形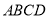 绕点
绕点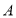 逆时针旋转
逆时针旋转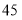 度后得到正方形
度后得到正方形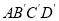 ,边
,边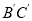 与
与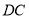 交于点
交于点 ,则四边形
,则四边形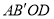 的周长是_______________.
的周长是_______________.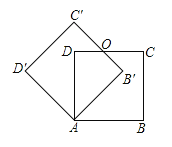
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣
 <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
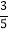 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PAPB的值称为点P关于⊙O的“幂值”
(1)⊙O的半径为6,OP=4.
①如图1,若点P恰为弦AB的中点,则点P关于⊙O的“幂值”为_____;
②判断当弦AB的位置改变时,点P关于⊙O的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P关于⊙0的“幂值”的取值范围;
(2)若⊙O的半径为r,OP=d,请参考(1)的思路,用含r、d的式子表示点P关于⊙O的“幂值”或“幂值”的取值范围_____;
(3)在平面直角坐标系xOy中,C(1,0),⊙C的半径为3,若在直线y=
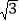 x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.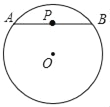
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知A(
 ,y1),B(2,y2)为反比例函数
,y1),B(2,y2)为反比例函数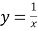 图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )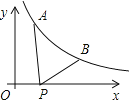
A. (
 ,0) B. (1,0) C. (
,0) B. (1,0) C. ( ,0) D. (
,0) D. ( ,0)
,0)
相关试题

