【题目】如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为( )

A. 54°B. 64°C. 74°D. 26°
参考答案:
【答案】B
【解析】
根据菱形的性质以及AM=CN,利用ASA可得△AMO≌△CNO,可得AO=CO,然后可得BO⊥AC,继而可求得∠OBC的度数.
∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
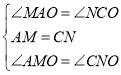 ,
,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=26°,
∴∠BCA=∠DAC=26°,
∴∠OBC=90°﹣26°=64°.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)在同一坐标系下,画出以上两个函数的图象.
(4)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
-
科目: 来源: 题型:
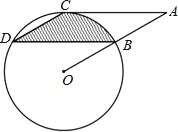
查看答案和解析>>【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
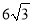 cm.
cm.(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
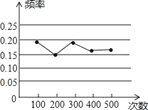
A. 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”
B. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
C. 掷一枚质地均匀的硬币,落地时结果是“正面朝上”
D. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果两个全等的三角形有一条公共边且位于公共边的异侧,我们称这两个三角形成轴全等,公共边所在直线称为全等轴.
(1)已知在平面直角坐标系中,△ABC的顶点A、B、C的坐标分别为(4,7)、(0,4)、(4,2),若△ACD与△ABC成轴全等,全等轴为直线AC,请直接写出D点坐标.
(2)如图,在平面直角坐标系中,△ABC两个顶点B、C坐标分别为(-14,0)、(
 ,0),∠ABC=45°,AC与y轴交于点E,点E的坐标为(0,
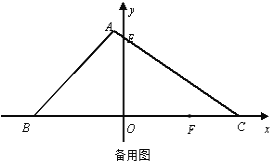
,0),∠ABC=45°,AC与y轴交于点E,点E的坐标为(0,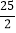 ),点F是OC上一点,坐标为(10,0) .如果M、N为△ABC的边上的两点,是否存在△OMN与△OFM以OM所在直线为全等轴的轴全等?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
),点F是OC上一点,坐标为(10,0) .如果M、N为△ABC的边上的两点,是否存在△OMN与△OFM以OM所在直线为全等轴的轴全等?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.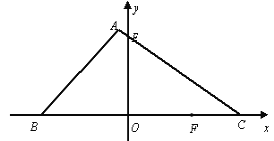
-
科目: 来源: 题型:
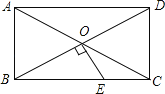
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,OE⊥BD交BC于点E,CD=1,则CE的长为( )
A.
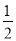 B.
B.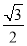 C.
C.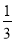 D.
D.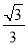
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为响应人民政府“形象重于生命”的号召,规划部门在甲建筑物的顶部
 点测得条幅顶端
点测得条幅顶端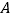 的仰角为
的仰角为 ,测得条幅底端的俯角为
,测得条幅底端的俯角为 ,已知条幅长
,已知条幅长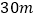 ,则底部不能直接到达的甲、乙两建筑物之间的水平距离
,则底部不能直接到达的甲、乙两建筑物之间的水平距离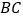 的长为________
的长为________ .(答案可带根号)
.(答案可带根号)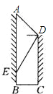
相关试题

