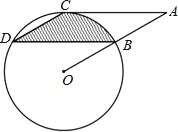
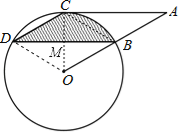
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
参考答案:
【答案】(1)证明见解析;(2)6πcm2.
【解析】试题分析:连接BC,OD,OC,设OC与BD交于点M.(1)求出∠COB的度数,求出∠A的度数,根据三角形的内角和定理求出∠OCA的度数,根据切线的判定推出即可;
(2)证明△CDM≌△OBM,从而得到S阴影=S扇形BOC.
试题解析:如图,连接BC,OD,OC,设OC与BD交于点M.
(1)根据圆周角定理得:∠COB=2∠CDB=2×30°=60°,∵AC∥BD,∴∠A=∠OBD=30°,∴∠OCA=180°﹣30°﹣60°=90°,即OC⊥AC,∵OC为半径,∴AC是⊙O的切线;
(2)由(1)知,AC为⊙O的切线,∴OC⊥AC.∵AC∥BD,∴OC⊥BD.由垂径定理可知,MD=MB=![]() BD=3
BD=3![]() .在Rt△OBM中,∠COB=60°,OB=
.在Rt△OBM中,∠COB=60°,OB=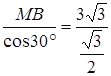 =6.
=6.
在△CDM与△OBM中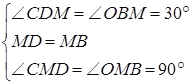 ,∴△CDM≌△OBM(ASA),∴S△CDM=S△OBM
,∴△CDM≌△OBM(ASA),∴S△CDM=S△OBM
∴阴影部分的面积S阴影=S扇形BOC=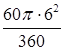 =6π(cm2).
=6π(cm2).
-
科目: 来源: 题型:
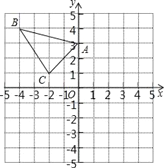
查看答案和解析>>【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
(1)容器内原有水多少?
(2)求W与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?

图 ① 图②
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)在同一坐标系下,画出以上两个函数的图象.
(4)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
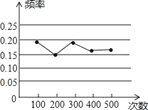
A. 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”
B. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
C. 掷一枚质地均匀的硬币,落地时结果是“正面朝上”
D. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为( )

A. 54°B. 64°C. 74°D. 26°
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果两个全等的三角形有一条公共边且位于公共边的异侧,我们称这两个三角形成轴全等,公共边所在直线称为全等轴.
(1)已知在平面直角坐标系中,△ABC的顶点A、B、C的坐标分别为(4,7)、(0,4)、(4,2),若△ACD与△ABC成轴全等,全等轴为直线AC,请直接写出D点坐标.
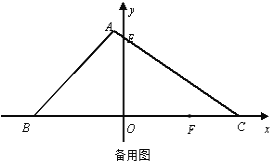
(2)如图,在平面直角坐标系中,△ABC两个顶点B、C坐标分别为(-14,0)、(
 ,0),∠ABC=45°,AC与y轴交于点E,点E的坐标为(0,
,0),∠ABC=45°,AC与y轴交于点E,点E的坐标为(0,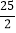 ),点F是OC上一点,坐标为(10,0) .如果M、N为△ABC的边上的两点,是否存在△OMN与△OFM以OM所在直线为全等轴的轴全等?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
),点F是OC上一点,坐标为(10,0) .如果M、N为△ABC的边上的两点,是否存在△OMN与△OFM以OM所在直线为全等轴的轴全等?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.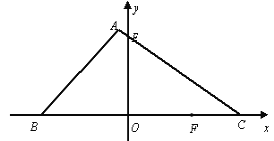
相关试题

