【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() 垂足为
垂足为![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)当![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若![]() 为
为![]() 中点,则当
中点,则当![]() 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形![]() 是正方形?请说明你的理由.
是正方形?请说明你的理由.
参考答案:
【答案】(1)见解析;(2)四边形![]() 是菱形.理由见解析;(3)当
是菱形.理由见解析;(3)当![]() 时,四边形
时,四边形![]() 是正方形.理由见解析.
是正方形.理由见解析.
【解析】
(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
(3)当∠A=45°,四边形BECD是正方形,只要证明![]() ,即可得到结论成立.
,即可得到结论成立.
![]() 证明:
证明:![]()
![]() ,
,
又![]() ,
,
![]()
![]()
又![]() ,即
,即![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() .
.
![]() 四边形
四边形![]() 是菱形.理由:
是菱形.理由:
![]() 为
为![]() 中点,
中点,
![]()
又由![]() 得
得![]()
![]()
又![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
又![]()
![]() 四边形
四边形![]() 是菱形;
是菱形;
![]() 当
当![]() 时,四边形
时,四边形![]() 是正方形;理由:
是正方形;理由:
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() 为
为![]() 中点,
中点,
![]() ,即
,即![]()
又![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() 四边形
四边形![]() 是正方形.
是正方形.
![]() 当
当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在
 中,
中, ,点
,点 为直线
为直线 上一动点(点
上一动点(点 不与点
不与点 重合).以
重合).以 为边作正方形
为边作正方形 连接
连接 .
.观察猜想:
(1)如图1,当点
 在线段
在线段 上时,判断
上时,判断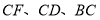 之间数量关系,并证明;
之间数量关系,并证明;


类比探究:
(2)如图2,当点
 在线段
在线段 的延长线上时,其他条件不变,请直接写出
的延长线上时,其他条件不变,请直接写出 三条线段之间的关系;
三条线段之间的关系;拓展延伸:
(3)如图3,当点
 在线段
在线段 的反向延长线上时,且点
的反向延长线上时,且点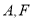 分别在直线
分别在直线 的两侧,其他条件不变;
的两侧,其他条件不变;①请直接写出
 三条线段之间的关系;
三条线段之间的关系;②若正方形
 的边长为
的边长为 、对角线
、对角线 相交于点
相交于点 ,连接
,连接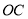 ,求
,求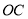 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B与∠C的角平分线相交于点I,过点I作BC的平行线,分别交AB、AC于点D、E.若AB=9,AC=6,BC=8,则△ADE的周长是( )
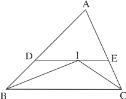
A. 14B. 15C. 17D. 23
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的角平分线,AD的中垂线交AB于点F,交BC的延长线于点E.以下四个结论:(1)∠EAD=∠EDA;(2)DF∥AC;(3)∠FDE=90°;(4)∠B=∠CAE.恒成立的结论有( )

A. (1)(2)B. (2)(3)(4)C. (1)(2)(4)D. (1)(2)(3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去等加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,
若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新特动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:AC=BE;
(2)若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

相关试题

