【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合).以
重合).以![]() 为边作正方形
为边作正方形![]() 连接
连接![]() .
.
观察猜想:
(1)如图1,当点![]() 在线段
在线段![]() 上时,判断
上时,判断![]() 之间数量关系,并证明;
之间数量关系,并证明;



类比探究:
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,其他条件不变,请直接写出
的延长线上时,其他条件不变,请直接写出![]() 三条线段之间的关系;
三条线段之间的关系;
拓展延伸:
(3)如图3,当点![]() 在线段
在线段![]() 的反向延长线上时,且点
的反向延长线上时,且点![]() 分别在直线
分别在直线![]() 的两侧,其他条件不变;
的两侧,其他条件不变;
①请直接写出![]() 三条线段之间的关系;
三条线段之间的关系;
②若正方形![]() 的边长为
的边长为![]() 、对角线
、对角线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,求
,求![]() 的长度.
的长度.
参考答案:
【答案】(1)![]() ;证明见解析;(2)
;证明见解析;(2)![]() ;(3)①
;(3)①![]() ,②
,② ![]() .
.
【解析】
(1)根据SAS证明△ABD≌△ACF,由△ABD≌△ACF的性质和线段的和可得结论;
(2)同理证明△ABD≌△ACF,可得BC⊥CF,由BD=BC+CD,BD=CF,可得新的结论:![]() ;
;
(3)①根据图3知:DC最长,同理:△DAB≌△FAC,则BD=CF,可得BC=DC-CF;
②先根据正方形的边长求对角线DF的长,证明∠DCF=90°,根据直角三角形斜边中线的性质可得OC的长.
证明:![]() ,
,![]() ,
,
![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,![]()
![]()
则在![]() 和
和![]() 中,
中,

![]() ,
,
![]()
![]() ,
,
![]() ;
;
(2)证明:如图2,
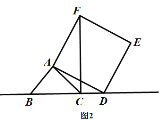
在正方形ADEF中,AD=AF,∠DAF=90°,
∵∠BAC=90°,
∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF,
∵∠ABC=45°,
∴∠ACB=180°-∠BAC-∠ABC=45°,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD与△ACF中,

∴△ABD≌△ACF,
∴∠ACF=∠ABD=45°,BD=CF,
∵∠ACB=45°,
∴∠BCF=∠ACB+∠ACF=90°,
∴BC⊥CF;
∵BD=BC+CD,BD=CF,
∴![]() ;
;
(3)①理由是:如图3,
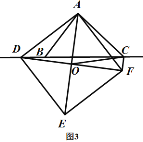
同理得:∠DAB=∠FAC,
与(2)同理,可证△DAB≌△FAC,
∴BD=CF,
∴DC=BD+BC=CF+BC,
∴BC=DC-CF;
![]() ,
,
![]()
![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]()
![]()
![]() 在
在![]() 和
和![]() 中,
中,

![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直角三角形.
是直角三角形.
![]() 正方形
正方形![]() 的边长为
的边长为![]()
且对角线![]() 相交于点
相交于点![]()
![]()
![]() 为
为![]() 中点.
中点.
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的图角如图3,则下列结论:①abc>0;②a+b+c=2;③a>
 ;④b<1.其中正确的结论是( )
;④b<1.其中正确的结论是( )
A. ①② B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A点坐标为(3,3),将△ABC 先向下平移4个单位得△A'B'C',再将△A'B'C'绕点O逆时针旋转180°得△A'B'C'.
(1)请你画出△A'B'C'和△A'B'C';
(2)点A'的坐标为 ;
(3)△ABC和△A'B'C'关于某个点中心对称,这个点的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】圆柱底面周长为4cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B与∠C的角平分线相交于点I,过点I作BC的平行线,分别交AB、AC于点D、E.若AB=9,AC=6,BC=8,则△ADE的周长是( )
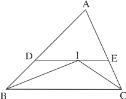
A. 14B. 15C. 17D. 23
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的角平分线,AD的中垂线交AB于点F,交BC的延长线于点E.以下四个结论:(1)∠EAD=∠EDA;(2)DF∥AC;(3)∠FDE=90°;(4)∠B=∠CAE.恒成立的结论有( )

A. (1)(2)B. (2)(3)(4)C. (1)(2)(4)D. (1)(2)(3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,过点
,过点 的直线
的直线 为
为 边上一点,过点
边上一点,过点 作
作 ,交直线
,交直线 于
于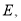 垂足为
垂足为 ,连接
,连接 .
.
(1)求证:
 ;
; (2)当
 为
为 中点时,四边形
中点时,四边形 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;(3)若
 为
为 中点,则当
中点,则当 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形 是正方形?请说明你的理由.
是正方形?请说明你的理由.
相关试题

