【题目】抛物线y=ax2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(﹣1,0).
(1)写出B点的坐标_____;
(2)若抛物线上存在一点P,使得△POC的面积是△BOC的面积的2倍,求点P的坐标;
(3)点M是线段BC上一点,过点M作x轴的垂线交抛物线于点D,求线段MD长度的最大值.
参考答案:
【答案】(3,0)
【解析】分析:(1)直接利用二次函数的对称性得出B点坐标即可;
(2)利用三角形面积求法结合抛物线上点的坐标性质得出答案;
(3)结合题意得出MD的函数关系式,进而得出答案.
详解:(1)∵抛物线y=ax2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(﹣1,0),
∴B点的坐标为:(3,0);
故答案为:(3,0);
(2)由抛物线y=ax2+bx+c的对称轴为直线x=1,A(﹣1,0),B(3,0),
则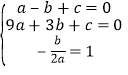 ,解得:
,解得: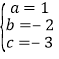 ,
,
故抛物线的表达式为y=x2﹣2x﹣3,
∴C(0,﹣3).
∴![]() .
.
∴S△POC=2S△BOC=9.
设点P的横坐标为xP,求得xP=±6.
代入抛物线的表达式,求得点P的坐标为(6,21),(﹣6,45).
(3)由点B(3,0),C(0,﹣3),得直线BC的表达式为y=x﹣3,

设点M(a,a﹣3),则点D(a,a2﹣2a﹣3).
∴MD=a﹣3﹣( a2﹣2a﹣3)
=﹣a2+3a
=![]() ,
,
∴当![]() 时,MD的最大值为
时,MD的最大值为![]() .
.
-
科目: 来源: 题型:
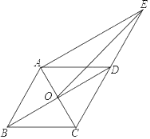
查看答案和解析>>【题目】已知菱形ABCD,对角线交点为O,延长CD至E且CD=DE.下列判断正确个数是( )
(1)∠AOB=90°;(2)AE=2OD;(3)∠OAE=90°;(4)∠AEO=∠CEO.
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王家购买了一套经济适用房,他家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
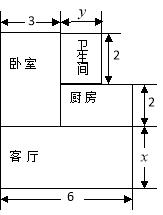
(1)写出用含
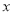 、
、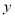 的代数式表示地面总面积;
的代数式表示地面总面积;(2)已知客厅面积比卫生间面积多21m2,且地面总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?
-
科目: 来源: 题型:
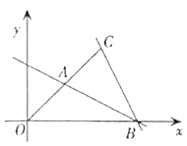
查看答案和解析>>【题目】已知在平面直角坐标系中,如图,点
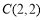 ,点
,点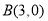 ,连接
,连接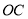 ,过点B作直线
,过点B作直线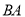 交
交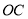 于A点,设直线
于A点,设直线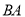 的解析式为
的解析式为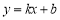
(1)求直线
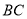 的函数关系式;
的函数关系式;(2)若直线
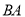 平分
平分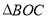 的面积时,求A到x轴的距离;
的面积时,求A到x轴的距离;(3)作点C关于y轴的对称点D,若直线
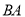 与线段
与线段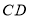 有交点,求k的取值范围.
有交点,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.下列结论正确的个数是( )
(1)t=5时,s=150;(2)t=35时,s=450;(3)甲的速度是30米/分;(4)t=12.5时,s=0.

A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
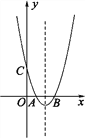
查看答案和解析>>【题目】如图,二次函数y=x2-4x+3的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求点A,点B和点D的坐标;
(2)在y轴上是否存在一点P,使PBC为等腰三角形?若存在,请求出点P的坐标;
(3)若动点M从点A出发,以每秒1个单位长度的速度沿AB向点B运动,同时另一个动点N从点D出发,以每秒2个单位长度的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,MNB的面积最大,试求出最大面积.

 (备用图)
(备用图) -
科目: 来源: 题型:
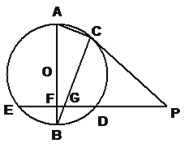
查看答案和解析>>【题目】已知,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
(1)求证:PC是⊙O的切线;
(2)若点C在劣弧AD上运动,其条件不变,问应再具备什么条件可使结论BG2=BF·BO成立,(要求画出示意图并说明理由).
相关试题

