【题目】如图,二次函数y=x2-4x+3的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求点A,点B和点D的坐标;
(2)在y轴上是否存在一点P,使PBC为等腰三角形?若存在,请求出点P的坐标;
(3)若动点M从点A出发,以每秒1个单位长度的速度沿AB向点B运动,同时另一个动点N从点D出发,以每秒2个单位长度的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,MNB的面积最大,试求出最大面积.

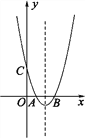 (备用图)
(备用图)
参考答案:
【答案】见解析
【解析】试题分析:(1)已知抛物线的一般式,令y=0,可得关于x的方程,解方程可得抛物线与x轴交点的横坐标,从而得到A、B两点坐标,通过配方可得到抛物线的对称轴,从而可得点D的坐标;
(2)先求出BC的长,然后分情况进行讨论即可得;
(3)设点M运动的时间为ts,用含t的式子先表示出BM与DN的长,然后利用三角形的面积公式表示出△MNB的面积,再根据二次函数的性质即可得.
试题解析:(1)当y=0时,x2-4x+3=0.
解得x1=1,x2=3,
∵点B在点A的右侧,∴点A的坐标为(1,0),点B的坐标为(3,0),
∵y=x2-4x+3=(x-2)2-1,
∴点D的坐标为(2,0);
(2)存在一点P,使△PBC为等腰三角形,
当x=0加法,y=x2-4x+3=3,∴点C的坐标为(0,3),
∴BC=![]() ,
,
点P中y轴上,当△PBC为等腰三角形时分三种情况讨论,点P位置如图,

①当CP=CB时,PC=3![]() ,
,
∴OP=OC+PC=3+3![]() 或OP=PC-OC=3
或OP=PC-OC=3![]() -3.
-3.
∴P1(0,3+3![]() ),P2(0,3-3
),P2(0,3-3![]() );
);
②当BP=BC时,OP=OC=3,
∴P3(0,-3);
③当PB=PC时,
∵OC=OB=3,
∴此时点P与点O重合.
∴P4(0,0),
综上所述,当点P的坐标为(0,3+3![]() )或(0,3-3
)或(0,3-3![]() )或(0,-3)或(0,0)时,△PBC为等腰三角形;
)或(0,-3)或(0,0)时,△PBC为等腰三角形;
(3)设点M运动的时间为ts,
∵AB=2,∴BM=2-t,DN=2t,
∴S△MNB=![]() =-t2+2t=-(t-1)2+1,
=-t2+2t=-(t-1)2+1,
∴当t=1时,△MNB的面积最大,最大面积为1,
此时M(2,0),N(2,2)或(2,-2),
∴当点M运动到(2,0),点N运动到(2,2)或(2,-2)时,△MNB的面积最大,最大面积为1.
-
科目: 来源: 题型:
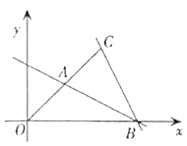
查看答案和解析>>【题目】已知在平面直角坐标系中,如图,点
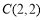 ,点
,点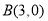 ,连接
,连接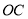 ,过点B作直线
,过点B作直线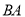 交
交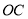 于A点,设直线
于A点,设直线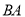 的解析式为
的解析式为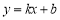
(1)求直线
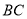 的函数关系式;
的函数关系式;(2)若直线
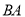 平分
平分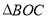 的面积时,求A到x轴的距离;
的面积时,求A到x轴的距离;(3)作点C关于y轴的对称点D,若直线
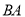 与线段
与线段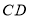 有交点,求k的取值范围.
有交点,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(﹣1,0).
(1)写出B点的坐标_____;
(2)若抛物线上存在一点P,使得△POC的面积是△BOC的面积的2倍,求点P的坐标;
(3)点M是线段BC上一点,过点M作x轴的垂线交抛物线于点D,求线段MD长度的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.下列结论正确的个数是( )
(1)t=5时,s=150;(2)t=35时,s=450;(3)甲的速度是30米/分;(4)t=12.5时,s=0.

A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
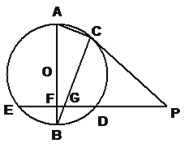
查看答案和解析>>【题目】已知,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
(1)求证:PC是⊙O的切线;
(2)若点C在劣弧AD上运动,其条件不变,问应再具备什么条件可使结论BG2=BF·BO成立,(要求画出示意图并说明理由).
-
科目: 来源: 题型:
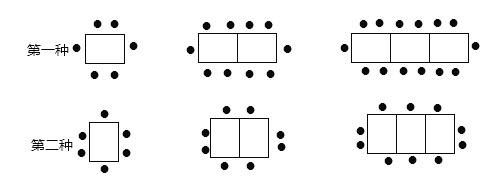
查看答案和解析>>【题目】(9分)某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐___________人;当有
 张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).(2)一天中午,餐厅要接待85位顾客共同就餐,但餐厅中只有20张这样的长方形桌子可用,且每4张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值.
(1)6a2-5a(a+2b-1)+a(-a+10b)+5,其中a=-1,b=2008;
(2)3xy2﹣[xy﹣2(2xy﹣
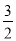 x2y)+2xy2]+3x2y,其中x、y满足(x+2)2+|y﹣1|=0.
x2y)+2xy2]+3x2y,其中x、y满足(x+2)2+|y﹣1|=0.
相关试题

