【题目】问题探究:在边长为![]() 的正方形
的正方形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .
.
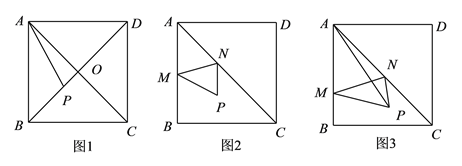
探究![]() :如图
:如图![]() ,若点
,若点![]() 是对角线
是对角线![]() 上任意一点,则线段
上任意一点,则线段![]() 的长的取值范围是__________;
的长的取值范围是__________;
探究![]() :如图
:如图![]() ,若点
,若点![]() 是
是![]() 内任意一点,点
内任意一点,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的值在探究
的值在探究![]() 中的取值范围内变化时,
中的取值范围内变化时, ![]() 的周长是否存在最小值?如果存在,请求出
的周长是否存在最小值?如果存在,请求出![]() 周长的最小值,若不存在,请说明理由;
周长的最小值,若不存在,请说明理由;
问题解决:如图![]() ,在边长为
,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是
是![]() 内任意一点,且
内任意一点,且![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的周长取到最小值时,求四边形
的周长取到最小值时,求四边形![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(![]() )
)![]() ;(
;(![]() )存在,2;(3)
)存在,2;(3)![]() .
.
【解析】试题分析:(1)当P与O重合时,PA的值最小,最小值为![]() ;当P与B或D重合时,PA的值最大,最大值为4,即可得线段
;当P与B或D重合时,PA的值最大,最大值为4,即可得线段![]() 的长的取值范围;(2)存在.如图2中,作点P关于AB、AC的对称点E、F,连接EF交AB于M,交AC于N,连接AE、AF、PA.由PM+MN+PN=EM+NM+NF=EF ,推出点P位置确定时,此时△PMN的周长最小,最小值为线段EF的长,由∠PAM=∠EAM,∠PAN=∠FAN,∠BAC=45°,推出∠EAF=2∠BAC=90°,由PA=PE=PF,推出△EAF 是等腰直角三角形,由PA的最小值为
的长的取值范围;(2)存在.如图2中,作点P关于AB、AC的对称点E、F,连接EF交AB于M,交AC于N,连接AE、AF、PA.由PM+MN+PN=EM+NM+NF=EF ,推出点P位置确定时,此时△PMN的周长最小,最小值为线段EF的长,由∠PAM=∠EAM,∠PAN=∠FAN,∠BAC=45°,推出∠EAF=2∠BAC=90°,由PA=PE=PF,推出△EAF 是等腰直角三角形,由PA的最小值为![]() ,可得线段EF的最小值为2,由此即可解决问题;(3)如图3中,在图2的基础上,以A为圆心AB为半径作⊙A ,PA交EF于点O.由△MAP≌△MAE, △NAP≌△NAF,推出
,可得线段EF的最小值为2,由此即可解决问题;(3)如图3中,在图2的基础上,以A为圆心AB为半径作⊙A ,PA交EF于点O.由△MAP≌△MAE, △NAP≌△NAF,推出![]() ,由此可以知道△AMN 的面积最小时,四边形AMPN的面积最大.
,由此可以知道△AMN 的面积最小时,四边形AMPN的面积最大.
试题解析:
(1)图1中,

∵四边形ABCD是正方形,边长为4,
∴AC⊥BD,AC=BD=4![]()
当P与O重合时,PA的值最小,最小值为2![]() ,
,
当P与B或D重合时,PA的值最大,最大值为4,
∴![]() ;
;
(2)存在.
理由:如图2中,作点P关于AB、AC的对称点E、F,连接EF交AB于M,交AC于N,连接AE、AF、PA.

∵PM+MN+PN=EM+NM+NF=EF,
∴点P位置确定时,此时的周长最小,最小值为线段EF的长,
∵∠PAM=∠EAM,∠PAN=∠FAN,∠BAC=45°,
∴∠EAF=2∠BAC=90°,
∵PA=PE=PF,
∴△EAF是等腰直角三角形,
∵PA的最小值为![]() ,
,
∴线段EF的最小值为2,
∴△PMN的周长的最小值为2.
(3)如图3中,在图2的基础上,以A为圆心AB为半径作⊙A,PA交EF于点O.
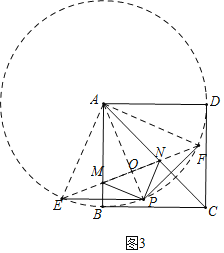
根据题意点P在上⊙A,
∵△MAP≌△MAE, △NAP≌△NAF,
∴![]()
∵PA=AE=AF=4,
∴![]() =8.
=8.
∴△AMN的面积最小时,四边形AMPN的面积最大,
易知当PA⊥MN时, △AMN 的面积最小,此时OA=![]() ,OM=ON=OP=4-
,OM=ON=OP=4-![]() ,
,
∴MN=8-4![]() ,
,
∴![]() ,
,
∴四边形AMPN的面积的最大值=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,
 ,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为_____.
,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与探究
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.请结合上述阅读材料,解决下列问题:

 在我们所学过的特殊四边形中,是勾股四边形的是________ (任写一种即可);
在我们所学过的特殊四边形中,是勾股四边形的是________ (任写一种即可); 图1、图2均为
图1、图2均为 的正方形网格,点
的正方形网格,点 均在格点上,请在图中标出格点
均在格点上,请在图中标出格点 ,连接
,连接 ,使得四边形
,使得四边形 符合下列要求:图1中的四边形
符合下列要求:图1中的四边形 是勾股四边形,并且是轴对称图形;图2中的四边形
是勾股四边形,并且是轴对称图形;图2中的四边形 是勾股四边形且对角线相等,但不是轴对称图形.
是勾股四边形且对角线相等,但不是轴对称图形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形
 中,
中, ,
, ,
, ,且
,且 ,
,试求:(1)
 的度数;(2)四边形
的度数;(2)四边形 的面积(结果保留根号);
的面积(结果保留根号);
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再解答问题:
已知在平面内有两点
 ,
,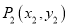 ,其两点间的距离公式为
,其两点间的距离公式为 ;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为 或
或 .
.(1)已知点A(2,4),B(-2,1),则AB=__________;
(2)已知点C,D在平行于y轴的直线上,点C的纵坐标为4,点D的纵坐标为-2,则CD=__________;
(3)已知点P(3,1)和(1)中的点A,B,判断线段PA,PB,AB中哪两条线段的长是相等的?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE,连接OC.
(1)求证:DE是⊙O的切线;
(2)若⊙O半径为4,∠D=30°,求图中阴影部分的面积(结果用含π和根号的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交于A、B(A在B左侧)两点, 一次函数y=-x+4与坐标轴分别交于点C、D,与抛物线交于点M、N,其中点M的横坐标是
与x轴交于A、B(A在B左侧)两点, 一次函数y=-x+4与坐标轴分别交于点C、D,与抛物线交于点M、N,其中点M的横坐标是 .
.(1)求出点C、D的坐标;
(2)求抛物线的表达式以及点A、B的坐标;
(3)在平面内存在动点P(P不与A,B重合),满足∠APB为直角,动点P到直线CD的距离是否有最小值,如果有,请直接写出这个最小值的结果;如果没有,请说明理由。

相关试题

