搜索
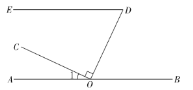
【题目】如图，点O在直线AB上，OC⊥OD，∠EDO与∠1互余．
（1）求证：ED//AB；
（2）OF平分∠COD交DE于点F，若∠OFD=65°，补全图形，并求∠1的度数．
参考答案：
【答案】（1）证明见解析；（2）补图见解析；20°
【解析】
（1）利用已知得出∠EDO+∠AOD=180°，进而得出答案；
（2）利用角平分线的定义结合已知得出∠COF=
∠COD=45°，进而得出答案．
（1）证明：∵∠EDO与∠1互余，
∴∠EDO+∠1=90°，
∵OC⊥OD，
∴∠COD=90°，
∴∠EDO+∠1+∠COD=180°，
∴∠EDO+∠AOD=180°，
∴ED∥AB；
（2）如图所示：
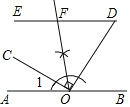
∵ED∥AB，
∴∠AOF=∠OFD=65°，
∵OF平分∠COD，
∴∠COF=∠COD=45°，
∴∠1=∠AOF-∠COF=20°．
-
科目： 来源： 题型：
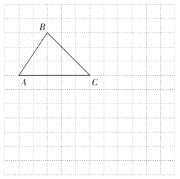
查看答案和解析>>【题目】在平面直角坐标系xOy中，△ABC的三个顶点分别是A（-2，0），B（0，3），C（3，0）.
（1）在所给的图中，画出这个平面直角坐标系；
（2）点A经过平移后对应点为D（3，-3），将△ABC作同样的平移得到△DEF，点B的对应点为点E，画出平移后的△DEF；
（3）在（2）的条件下，点M在直线CD上，若DM=2CM，直接写出点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“构造图形解题”，它的应用十分广泛，特别是有些技巧性很强的题目，如果不能发现题目中所隐含的几何意义，而用通常的代数方法去思考，经常让我们手足无措，难以下手，这时，如果能转换思维，发现题目中隐含的几何条件，通过构造适合的几何图形，将会得到事半功倍的效果，下面介绍两则实例：
实例一：1876年，美国总统伽非尔德利用实例一图证明了勾股定理：由
S四边形ABCD=S△ABC+S△ADE+S△ABE得
，化简得：
实例二：欧几里得的《几何原本》记载，关于x的方程
的图解法是：画Rt△ABC，使∠ABC=90°，BC=
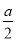，AC=
，再在斜边AB上截取BD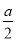＝，则AD的长就是该方程的一个正根(如实例二图)请根据以上阅读材料回答下面的问题：
(1)如图1，请利用图形中面积的等量关系，写出甲图要证明的数学公式是 ，乙图要证明的数学公式是
(2)如图2，若2和-8是关于x的方程x2+6x＝16的两个根，按照实例二的方式构造Rt△ABC，连接CD，求CD的长；
(3)若x，y，z都为正数，且x2+y2＝z2，请用构造图形的方法求
的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
的顶点坐标为
，并且与
轴交于点
，与
轴交于
、
两点．（
）求抛物线的表达式．（
）如图
，设抛物线的对称轴与直线
交于点
，点
为直线
上一动点，过点
作
轴的平行线
，与抛物线交于点
，问是否存在点
，使得以
、
、
为顶点的三角形与
相似．若存在，求出点
的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，
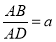，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．（1）如图1，当DH=DA时，
①填空：∠HGA= 度；
②若EF∥HG，求∠AHE的度数，并求此时a的最小值；
（2）如图3，∠AEH=60°，EG=2BG，连接FG，交边FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，菱形ABCD的边长为2，
，点E为BC边的中点，点P为对角线AC上一动点，则PB+PE的最小值为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读与探究
我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．请结合上述阅读材料，解决下列问题：
在我们所学过的特殊四边形中，是勾股四边形的是________ (任写一种即可)；
图1、图2均为
的正方形网格，点
均在格点上，请在图中标出格点
，连接
，使得四边形
符合下列要求：图1中的四边形是勾股四边形，并且是轴对称图形；图2中的四边形是勾股四边形且对角线相等，但不是轴对称图形．
相关试题
