【题目】在矩形ABCD中,![]() ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
(1)如图1,当DH=DA时,
①填空:∠HGA= 度;
②若EF∥HG,求∠AHE的度数,并求此时a的最小值;
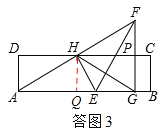
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.

参考答案:
【答案】(1)①45;②当∠AHE为锐角时,∠AHE=22.5°时,a的最小值是2;当∠AHE为钝角时,∠AHE=112.5°时,a的最小值是![]() ;(2)
;(2)![]() .
.
【解析】
(1)①∵四边形ABCD是矩形,∴∠ADH=90°.
∵DH=DA,∴∠DAH=∠DHA=45°.∴∠HAE=45°.
∵HA=HG,∴∠HAE=∠HGA=45°
②分两种情况讨论:
第一种情况:如答图1,∠AHE为锐角时,
∵∠HAG=∠HGA=45°,∴∠AHG=90°.
由折叠可知:∠HAE=∠F=45°,∠AHE=∠FHE,
∵EF∥HG,∴∠FHG=∠F=45°.
∴∠AHF=∠AHG![]() ∠FHG=45°,即∠AHE+∠FHE=45°.
∠FHG=45°,即∠AHE+∠FHE=45°.
∴∠AHE=22.5°.
此时,当B与G重合时,a的值最小,最小值是2.

第二种情况:如答图2,∠AHE为钝角时,
∵EF∥HG,∴∠HGA=∠FEA=45°,即∠AEH+∠FEH=45°.
由折叠可知:∠AEH=∠FEH,∴∠AEH=∠FEH=22.5°.
∵EF∥HG,∴∠GHE=∠FEH=22.5°.
∴∠AHE=90°+22.5°=112.5°.
此时,当B与E重合时,a的值最小,
设DH=DA=x,则AH=CH=![]() x,
x,
在Rt△AHG中,∠AHG=90°,由勾股定理得:AG=![]() AH=2x,
AH=2x,
∵∠AEH=∠FEH,∠GHE=∠FEH,∴∠AEH=∠GHE.∴GH=GE=![]() x.
x.
∴AB=AE=2x+![]() x.
x.
∴a的最小值是![]() .
.
综上所述,当∠AHE为锐角时,∠AHE=22.5°时,a的最小值是2;当∠AHE为钝角时,∠AHE=112.5°时,a的最小值是![]() .
.

(2)如答图3:过点H作HQ⊥AB于Q,则∠AQH=∠GQH=90°,
在矩形ABCD中,∠D=∠DAQ=90°,
∴∠D=∠DAQ=∠AQH=90°.
∴四边形DAQH为矩形.∴AD=HQ.
设AD=x,GB=y,则HQ=x,EG=2y,
由折叠可知:∠AEH=∠FEH=60°,∴∠FEG=60°.
在Rt△EFG中,EG=EF×cos60°=2y,
在Rt△HQE中,![]() ,
,
∴![]() .
.
∵HA=HG,HQ⊥AB,∴AQ=GQ=![]() .
.
∴AE=AQ+QE=![]() .
.
由折叠可知:AE=EF,即![]() ,即
,即![]() .
.
∴AB=2AQ+GB= .
.
∴ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“构造图形解题”,它的应用十分广泛,特别是有些技巧性很强的题目,如果不能发现题目中所隐含的几何意义,而用通常的代数方法去思考,经常让我们手足无措,难以下手,这时,如果能转换思维,发现题目中隐含的几何条件,通过构造适合的几何图形,将会得到事半功倍的效果,下面介绍两则实例:
实例一:1876年,美国总统伽非尔德利用实例一图证明了勾股定理:由
S四边形ABCD=S△ABC+S△ADE+S△ABE得
 ,化简得:
,化简得:
实例二:欧几里得的《几何原本》记载,关于x的方程
 的图解法是:
的图解法是:画Rt△ABC,使∠ABC=90°,BC=
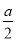 ,AC=
,AC= ,再在斜边AB上截取BD=
,再在斜边AB上截取BD=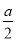 ,则AD的长就是该方程的一个正根(如实例二图)
,则AD的长就是该方程的一个正根(如实例二图)请根据以上阅读材料回答下面的问题:
(1)如图1,请利用图形中面积的等量关系,写出甲图要证明的数学公式是 ,乙图要证明的数学公式是
(2)如图2,若2和-8是关于x的方程x2+6x=16的两个根,按照实例二的方式构造Rt△ABC,连接CD,求CD的长;
(3)若x,y,z都为正数,且x2+y2=z2,请用构造图形的方法求
 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的顶点坐标为
的顶点坐标为 ,并且与
,并且与 轴交于点
轴交于点 ,与
,与 轴交于
轴交于 、
、 两点.
两点.(
 )求抛物线的表达式.
)求抛物线的表达式.(
 )如图
)如图 ,设抛物线的对称轴与直线
,设抛物线的对称轴与直线 交于点
交于点 ,点
,点 为直线
为直线 上一动点,过点
上一动点,过点 作
作 轴的平行线
轴的平行线 ,与抛物线交于点
,与抛物线交于点 ,问是否存在点
,问是否存在点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似.若存在,求出点
相似.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
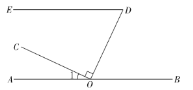
查看答案和解析>>【题目】如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,
 ,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为_____.
,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与探究
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.请结合上述阅读材料,解决下列问题:

 在我们所学过的特殊四边形中,是勾股四边形的是________ (任写一种即可);
在我们所学过的特殊四边形中,是勾股四边形的是________ (任写一种即可); 图1、图2均为
图1、图2均为 的正方形网格,点
的正方形网格,点 均在格点上,请在图中标出格点
均在格点上,请在图中标出格点 ,连接
,连接 ,使得四边形
,使得四边形 符合下列要求:图1中的四边形
符合下列要求:图1中的四边形 是勾股四边形,并且是轴对称图形;图2中的四边形
是勾股四边形,并且是轴对称图形;图2中的四边形 是勾股四边形且对角线相等,但不是轴对称图形.
是勾股四边形且对角线相等,但不是轴对称图形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形
 中,
中, ,
, ,
, ,且
,且 ,
,试求:(1)
 的度数;(2)四边形
的度数;(2)四边形 的面积(结果保留根号);
的面积(结果保留根号);
相关试题

