【题目】如图,将一张矩形纸片沿着AE折叠后,点D恰好与BC边上的点F重合,已知AB=6cm,BC=10cm,则EC的长度为_____cm.

参考答案:
【答案】3.
【解析】
先根据翻折变换的性质得出Rt△ADE≌Rt△AEF,再先设EC的长为x,则AF=10cm,EF=DE=(8﹣x)cm,在Rt△ABF中由勾股定理得:AB2+BF2=AF2,已知AB、AF的长可求出BF的长,又CF=BC﹣BF=10﹣BF,在Rt△ECF中由勾股定理可得:EF2=EC2+CF2,即:(8﹣x)2=x2+(10﹣BF)2,将求出的BF的值代入该方程求出x的值,即求出了EC的长.
解:∵△AEF由△ADE翻折而成,
∴Rt△ADE≌Rt△AEF,
∴∠AFE=90°,AD=AF=10cm,EF=DE,
设EC=xcm,则DE=EF=CD﹣EC=(8﹣x)cm,
在Rt△ABF中由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC﹣BF=10﹣6=4(cm),
在Rt△ECF中由勾股定理可得:EF2=EC2+CF2,
即(8﹣x)2=x2+42,
∴64﹣16x+x2=x2+16,
∴x=3(cm),即EC=3cm,
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价
 (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)(2)当每盒售价定为多少元时,每天销售的利润
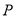 (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:二元一次方程
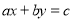 有无数组解,每组解记为
有无数组解,每组解记为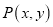 ,称
,称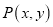 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:(1) 已知
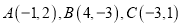 ,则是隐线
,则是隐线 的亮点的是 ;
的亮点的是 ;(2) 设
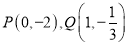 是隐线
是隐线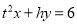 的两个亮点,求方程
的两个亮点,求方程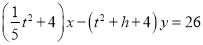 中
中 的最小的正整数解;
的最小的正整数解;(3)已知
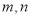 是实数, 且
是实数, 且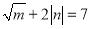 ,若
,若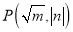 是隐线
是隐线 的一个亮点,求隐线
的一个亮点,求隐线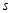 中的最大值和最小值的和.
中的最大值和最小值的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面坐标系中,
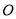 为原点,直线
为原点,直线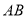 交
交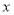 轴正半轴于点
轴正半轴于点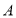 ,交
,交 轴正半轴于点
轴正半轴于点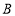 .
.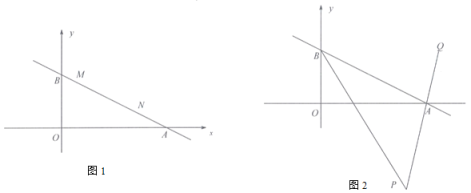
(1) 如图1,直线
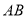 上有
上有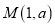 和
和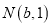 两点,
两点,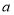 的相反数是
的相反数是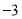 ,
,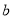 是
是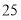 的算术平方根,求:
的算术平方根,求:①
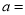 ____ ;
____ ; 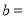 _____ ; ②点
_____ ; ②点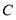 在
在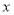 轴正半轴上运动,使得
轴正半轴上运动,使得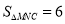 ,则点
,则点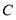 的坐标为 .
的坐标为 .(2)如图2, 若
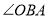 的平分线
的平分线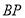 与
与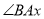 的平分线
的平分线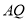 反向延长线交于点
反向延长线交于点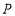 ,设
,设 ,求证:
,求证: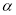 的值为定值;
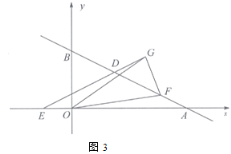
的值为定值;(3)如图3,
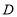 在直线
在直线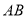 上,
上, 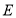 在
在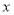 轴上,在
轴上,在 中,始终满足以下条件:
中,始终满足以下条件: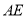 为最大边,
为最大边, 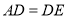 ,当
,当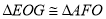 时,求
时,求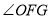 的取值范围.
的取值范围. -
科目: 来源: 题型:
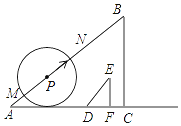
查看答案和解析>>【题目】如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60cm,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿
CA方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与直线AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中:
(1)连接ME,当ME∥AC时,t=________s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 .
.(2)
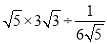 .
.(3)
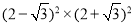 .
.(4)
 .(利用幂的运算性质计算)
.(利用幂的运算性质计算)(5)
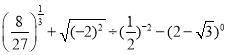 .
.
相关试题

