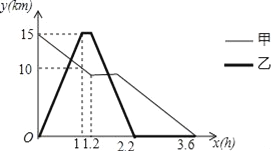
【题目】某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.
(2)求甲、乙第一次相遇的时间.
(3)直接写出乙回到侧门时,甲到侧门的路程.
参考答案:
【答案】(1)y=﹣5x+15;(2)0.75h;(3)7km.
【解析】(1)根据函数图象可知点(0,15)和点(1,10)在甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数图象上,从而可以解答本题;
(2)根据函数图象可以分别求得甲乙刚开始两端对应的函数解析式,联立方程组即可求得第一次相遇的时间;
(3)根据函数图象可以得到在最后一段甲对应的函数解析式,乙到侧门时时间为2.2h,从而可以得到乙回到侧门时,甲到侧门的路程.
解:(1)设甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式为:y=kx+b,
∵点(0,15)和点(1,10)在此函数的图象上,
∴![]() ,
,
解得k=﹣5,b=15.
∴y=﹣5x+15.
即甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式为:y=﹣5x+15.
(2)设乙骑自行车从侧门匀速前往正门对应的函数关系式y=kx,
将(1,15)代入可得k=15,
∴乙骑自行车从侧门匀速前往正门对应的函数关系式y=15x,
∴![]() , 解得x=0.75.
, 解得x=0.75.
即第一次相遇时间为0.75h.
(3)乙回到侧门时,甲到侧门的路程是7km.
设甲休息了0.6小时后仍按原速继续行走对应的函数解析式为:y=kx+b.
将x=1.2代入y=﹣5x+15得,y=9.
∵点(1.8,9),(3.6,0)在y=kx+b上,
∴![]() ,
,
解得k=﹣5,b=18.
∴y=﹣5x+18.
将x=2.2代入y=﹣5x+18,得y=7.
即乙回到侧门时,甲到侧门的路程是7km.
“点睛”本题考查一次函数的应用,解题的关键是能看懂题意,根据数形结合的数学思想,找出所求问题需要的条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、B、F、C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )

A. AB=DE B. DF∥AC C. ∠E=∠ABC D. AB∥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一副三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=()度。
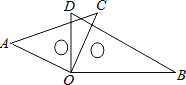
A. 小于180 B. 大于180 C. 等于180 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两个条件:①y随x的增大而减小;②图象经过点(1,2).写出1个同时具备条件①、②的一个一次函数表达式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在通常的日历牌上,可以看到一些数满足的规律,表①是2017年10月份的日历牌
周日
周一
周二
周三
周四
周五
周六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

(表①)
(1)在表①中,我们选择如表②那样的平行四边形框任意圈出2×2个数,将它们交叉相加,如:用平行四边形框圈出2、3、8、9四个数,然后将它们交叉相加后发现3+8=2+9,用表②的平行四边形框任意圈出2×2个数(与2、3、8、9四个数不同),将它们交叉相加,然后列出相应的等式.
(2)在用表②的平行四边形框任意圈出的2×2个数中,若设左上角的数字为
 ,用含
,用含 的代数式表示这四个数的和.
的代数式表示这四个数的和.(3)用表③的平行四边形框任意圈出9个数.
①若设最中间的数字为n,求表③的平行四边形框任意圈出9个数和(用含n的代数式表示)
②若圈出的9个数的和是108.则这个平行四边形框的右上角表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】教师运动会中,甲,乙两组教师参加“两人背夹球”往返跑比赛,即:每组两名教师用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.若距起点的距离用y(米)表示,时间用x(秒)表示.下图表示两组教师比赛过程中y与x的函数关系的图象.根据图象,有以下四个推断:
①乙组教师获胜
②乙组教师往返用时相差2秒
③甲组教师去时速度为0.5米/秒
④返回时甲组教师与乙组教师的速度比是2:3
其中合理的是( )
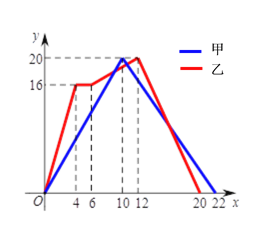
A. ①② B. ①③ C. ②④ D. ①④
相关试题

