【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求点E的坐标.

参考答案:
【答案】(1)见解析 (2)(4.5,1).
【解析】(1)易证四边形AEBD是平行四边形,再证明临边DA=DB即可;
(2)连接DE,交AB于点F,分别求出EF,AF的长即可求出点E的坐标.
解:(1)证明:
∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形.
又∵四边形OABC是矩形,
∴OB=AC,且互相平分,
∴DA=DB.
∴四边形AEBD是菱形.
(2)连接DE,交AB于点F.
由(1)四边形AEBD是菱形,
∴AB与DE互相垂直平分于点F.
又∵OA=3,OC=2,
∴EF=DF=![]() OA=1.5,AF=
OA=1.5,AF=![]() AB=1.
AB=1.
∴E点坐标为(4.5,1).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
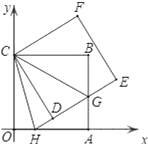
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、B、F、C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )

A. AB=DE B. DF∥AC C. ∠E=∠ABC D. AB∥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一副三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=()度。
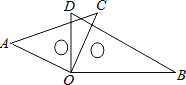
A. 小于180 B. 大于180 C. 等于180 D. 无法确定
-
科目: 来源: 题型:
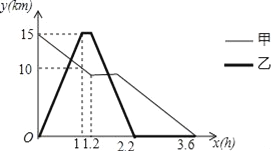
查看答案和解析>>【题目】某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.
(2)求甲、乙第一次相遇的时间.
(3)直接写出乙回到侧门时,甲到侧门的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两个条件:①y随x的增大而减小;②图象经过点(1,2).写出1个同时具备条件①、②的一个一次函数表达式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在通常的日历牌上,可以看到一些数满足的规律,表①是2017年10月份的日历牌
周日
周一
周二
周三
周四
周五
周六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

(表①)
(1)在表①中,我们选择如表②那样的平行四边形框任意圈出2×2个数,将它们交叉相加,如:用平行四边形框圈出2、3、8、9四个数,然后将它们交叉相加后发现3+8=2+9,用表②的平行四边形框任意圈出2×2个数(与2、3、8、9四个数不同),将它们交叉相加,然后列出相应的等式.
(2)在用表②的平行四边形框任意圈出的2×2个数中,若设左上角的数字为
 ,用含
,用含 的代数式表示这四个数的和.
的代数式表示这四个数的和.(3)用表③的平行四边形框任意圈出9个数.
①若设最中间的数字为n,求表③的平行四边形框任意圈出9个数和(用含n的代数式表示)
②若圈出的9个数的和是108.则这个平行四边形框的右上角表示的数是 .
相关试题

