【题目】如图所示,E、B、F、C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )

A. AB=DE B. DF∥AC C. ∠E=∠ABC D. AB∥DE
参考答案:
【答案】A
【解析】由EB=CF,可得出EF=BC,又有∠A=∠D,本题具备了一组边、一组角对应相等,为了再添一个条件仍不能证明△ABC≌△DEF,那么添加的条件与原来的条件可形成SSA,就不能证明△ABC≌△DEF了.
解:添加选项A中的DE=AB与原条件满足SSA,不能证明△ABC≌△DEF.
添加选项B中的DF∥AC,可得∠DFE=∠ACB,根据AAS能证明△ABC≌△DEF.
添加选项C中的∠E=∠ABC,根据AAS能证明△ABC≌△DEF.
添加选项D中的AB∥DE,可得∠E=∠ABC,根据AAS能证明△ABC≌△DEF.
故选A.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题:
(1)在表中的频数分布表中,m= ,n= .
成绩
频数
频率
60≤x<70
60
0.30
70≤x<80
m
0.40
80≤x<90
40
n
90≤x≤100
20
0.10
(2)请补全图中的频数分布直方图.
(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=
 x+4的图像与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=
x+4的图像与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y= 的图像在第一象限经过点A.
的图像在第一象限经过点A.(1)求点A的坐标以及k的值:
(2)点P是反比例函数y=
 (x>0)的图像上一点,且△PAO的面积为21,求点P的坐标.
(x>0)的图像上一点,且△PAO的面积为21,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
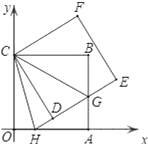
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一副三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=()度。
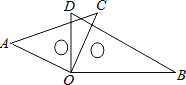
A. 小于180 B. 大于180 C. 等于180 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求点E的坐标.

-
科目: 来源: 题型:
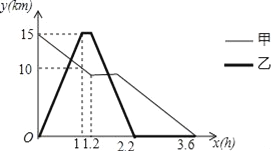
查看答案和解析>>【题目】某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.
(2)求甲、乙第一次相遇的时间.
(3)直接写出乙回到侧门时,甲到侧门的路程.
相关试题

