【题目】如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF
解:∵AB∥CD,(已知)
∴∠AMN=∠DNM()
∵ME、NF分别是∠AMN、∠DNM的角平分线,(已知)
∴∠EMN=∠AMN,
∠FNM=∠DNM (角平分线的定义)
∴∠EMN=∠FNM(等量代换)
∴ME∥NF()
由此我们可以得出一个结论:
两条平行线被第三条直线所截,一对角的平分线互相 .
参考答案:
【答案】两直线平行,内错角相等;![]() ;
;![]() ;内错角相等,两直线平行;内角;平行
;内错角相等,两直线平行;内角;平行
【解析】此题考查平行线的性质和角平分线的定义的运用;并考查学生对证明题的条件及结论的总结.
【考点精析】本题主要考查了角的平分线和平行线的判定与性质的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.
-
科目: 来源: 题型:
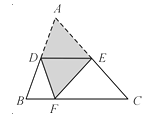
查看答案和解析>>【题目】如图,将三角形ABC沿DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70,则∠BDF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2a3b﹣4a2b2+2ab3=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A的余角是32°,则∠A= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
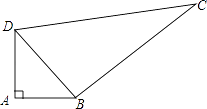
(1)试判断△BCD的形状;
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮? -
科目: 来源: 题型:
查看答案和解析>>【题目】在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
(1)请你作出平移后的图形△DEF,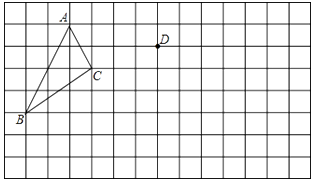
(2)请求出△DEF的面积。 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:1012-202+1.
相关试题

