【题目】如图,数轴上点A对应的有理数为20,点P以每秒2个单位长度的速度从点A出发,点Q以每秒4个单位长度的速度从原点O出发,且P,Q两点同时向数轴正方向运动,设运动时间为t秒. ![]()
(1)当t=2时,P,Q两点对应的有理数分别是 , , PQ=;
(2)当PQ=10时,求t的值.
参考答案:
【答案】
(1)24;8;16
(2)解:①当点P在点Q右侧时,
PQ=(20+2t)﹣4t=10,
解得:t=5;
②当点P在点Q左侧时,
PQ=4t﹣(20+2t)=10,
解得:t=15.
综上所述,t的值为5秒或15秒
【解析】解:(1)∵20+2×2=24,4×2=8, ∴当t=2时,P,Q两点对应的有理数分别是24,8,
∴PQ=24﹣8=16.
所以答案是:24;8;16.
【考点精析】关于本题考查的数轴和代数式求值,需要了解数轴是规定了原点、正方向、单位长度的一条直线;求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】扇形统计图中,某部分所对应的扇形圆心角为36°,则该部分所占总体的百分比_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
 ≈1.7)
≈1.7)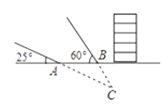
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )
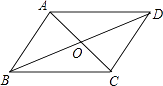
A.6
B.2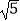
C.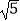
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D , 交AB于点E , 且BE=BF , 添加一个条件,仍不能证明四边形BECF为正方形的是( ).
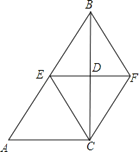
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
相关试题

