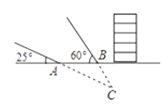
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7)
参考答案:
【答案】3.
【解析】试题分析:过C点作AB的垂线交AB的延长线于点D,通过解Rt△ADC得到AD=2CD=2x,在Rt△BDC中利用锐角三角函数的定义即可求出CD的值.
试题解析:作CD⊥AB交AB延长线于D,设CD=x米.

Rt△ADC中,∠DAC=25°,
所以tan25°=![]() =0.5,
=0.5,
所以AD=![]() =2x
=2x
Rt△BDC中,∠DBC=60°,
由tan 60°=![]() =
=![]() ,
,
解得:x≈3.
所以生命迹象所在位置C的深度约为3米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
A.
B.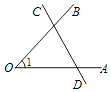
C.
D.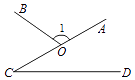
-
科目: 来源: 题型:
查看答案和解析>>【题目】扇形统计图中,某部分所对应的扇形圆心角为36°,则该部分所占总体的百分比_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A对应的有理数为20,点P以每秒2个单位长度的速度从点A出发,点Q以每秒4个单位长度的速度从原点O出发,且P,Q两点同时向数轴正方向运动,设运动时间为t秒.
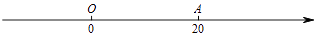
(1)当t=2时,P,Q两点对应的有理数分别是 , , PQ=;
(2)当PQ=10时,求t的值. -
科目: 来源: 题型:
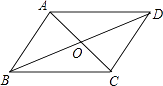
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )
A.6
B.2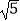
C.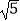
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
相关试题

