【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
参考答案:
【答案】(1)直线l与⊙O相切;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)连接OE、OB、OC.由题意可证明![]() ,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;
,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;
(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;
(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF的长.
试题解析:(1)直线l与⊙O相切.理由如下:
如图1所示:连接OE、OB、OC.
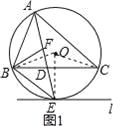
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∴![]() .
.
∴∠BOE=∠COE.
又∵OB=OC,
∴OE⊥BC.
∵l∥BC,
∴OE⊥l.
∴直线l与⊙O相切.
(2)∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵∠CBE=∠CAE=∠BAE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB.
∴BE=EF.
(3)由(2)得BE=EF=DE+DF=7.
∵∠DBE=∠BAE,∠DEB=∠BEA,
∴△BED∽△AEB.
∴![]() ,即
,即![]() ,解得;AE=
,解得;AE=![]() ,
,
∴AF=AE﹣EF=![]() ﹣7=
﹣7=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四位学生用计算器求sin62°20′的值正确的是( )
A.0.8857
B.0.8856
C.0.8852
D.0.8851 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
A.
B.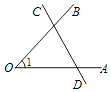
C.
D.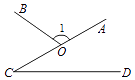
-
科目: 来源: 题型:
查看答案和解析>>【题目】扇形统计图中,某部分所对应的扇形圆心角为36°,则该部分所占总体的百分比_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
 ≈1.7)
≈1.7)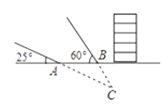
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A对应的有理数为20,点P以每秒2个单位长度的速度从点A出发,点Q以每秒4个单位长度的速度从原点O出发,且P,Q两点同时向数轴正方向运动,设运动时间为t秒.
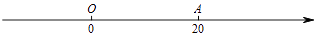
(1)当t=2时,P,Q两点对应的有理数分别是 , , PQ=;
(2)当PQ=10时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )
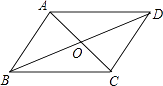
A.6
B.2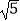
C.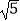
D.3
相关试题

