Question

【题目】已知△ABC中，

（1）点O在线段AB上，以点O为圆心，AO为半径作⊙O，⊙O经过点C。

（要求尺规作图，保留作图痕迹，写结论，不必写作法。）

（2）若∠A=25°，∠B=40°，请判断BC与⊙O的位置关系并写出证明过程。

Answer 1

【答案】（1）作图见解析；（2）理由见解析.

【解析】试题分析：（1）利用基本作图（作已知线段的垂直平分线）作线段AB的垂直平分线l；
（2）连结OC，如图，根据线段垂直平分线的性质得∠A=∠OCA=25°，再利用三角形外角性质得∠BOC=50°，接着根据三角形内角和可计算出∠BCO=90°，然后根据切线的判定定理即可判断BC为⊙O的切线．

试题解析：（1）如图，直线l为所求；

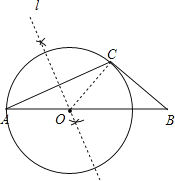
（2）⊙O为所求．

BC与⊙O相切．理由如下：

连结OC，如图，

∵直线l垂直平分AC，

∴∠A=∠OCA=25°，

∴∠BOC=∠A+∠OCA=50°，

∵∠B=40°，

∴∠BCO=180°﹣∠BOC﹣∠B=90°，

∴OC⊥BC，

∴BC为⊙O的切线．