【题目】某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.设租用时间为![]() 个月,所需租金为
个月,所需租金为![]() 元.
元.
(1)请分别写出租用甲、乙两家房屋的租金![]() 与租用时间
与租用时间![]() 之间的函数关系;
之间的函数关系;
(2)试判断租用哪家房屋更合算,请写出详细分析过程.
参考答案:
【答案】(1)租用甲家房屋时:y=3000x;租用乙家房屋时:y=2000x+40000;(2)①当租用40个月时,两家租金相同;②当租用时间超过40个月时,租乙家的房屋更合算;③当租用时间少于40个月时,租甲家的房屋更合算.
【解析】
(1)根据题目的关系,即可求出关系式;
(2)令甲、乙两家租金相等时,求出月数,然后再进行分析即可.
解:(1)根据题意,
租用甲家房屋时:y=3000x;
租用乙家房屋时:y=2000x+40000;
(2)①由题意,可知:
3000x=2000x+40000,
解得: x=40,
即当租用40个月时,两家租金相同.
②由3000x>2000x+40000,
解得: x>40;
即当租用时间超过40个月时,租乙家的房屋更合算.
③由3000x<2000x+40000,
解得: x<40
即当租用时间少于40个月时,租甲家的房屋更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在探究一次函数
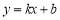 的图像性质时我们有如下发现:
的图像性质时我们有如下发现:①系数
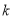 决定了函数图像的坡度,
决定了函数图像的坡度,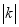 越大则图像坡度越大(越靠近
越大则图像坡度越大(越靠近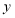 轴),
轴),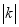 越小则图像坡度越小(越靠近
越小则图像坡度越小(越靠近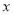 轴);
轴);②常数项
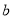 决定了图像与
决定了图像与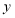 轴的交点,即函数图像与
轴的交点,即函数图像与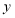 轴交点坐标始终为
轴交点坐标始终为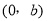 .
.基于以上发现,我们得出结论:如果两个一次函数的
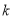 值相同,那么两个一次函数的图像平行.反之,如果两直线平行,则两条直线所对应的函数表达式的
值相同,那么两个一次函数的图像平行.反之,如果两直线平行,则两条直线所对应的函数表达式的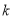 值一定相等:把函数图像沿
值一定相等:把函数图像沿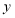 轴向上(或向下) 平移
轴向上(或向下) 平移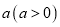 个单位, 系数
个单位, 系数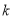 保持不变, 常数
保持不变, 常数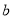 变为
变为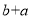 (或
(或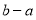 ).如:函数
).如:函数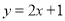 和
和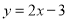 的图像互相平行:函数
的图像互相平行:函数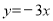 的图像向上平移2个单位后所得函数表达式为
的图像向上平移2个单位后所得函数表达式为 .
.据此回答下列问题:
(1) 把函数
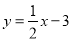 的图像向上平移4个单位后所得函数的表达式为____;
的图像向上平移4个单位后所得函数的表达式为____;(2)把函数
 的图像向 (上或下)平移 个单位可得到函数
的图像向 (上或下)平移 个单位可得到函数 的图像;
的图像;(3)若直线
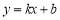 经过点
经过点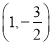 且与直线
且与直线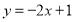 平行,求出直线
平行,求出直线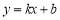 的表达式.
的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并回答问题.我们知道|a|的几何意义是指数轴上表示数的点与原点的距离,那么|a-b|的几何意义又是什么呢?我们不妨考虑一下,取特殊值时的情况.比如考虑|5-(-6)|的几何意义,在数轴上分别标出表示-6和5的点,(如图所示),两点间的距离是11,而|5-(-6)|=11,因此不难看出|5-(-6)|就是数轴上表示-6和5两点间的距离.
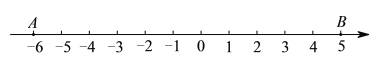
(1)|a-b|的几何意义是_______;
(2)当|x-2|=2时,求出x的值.
(3)设Q=|x+6|-|x-5|,请问Q是否存在最大值,若没有请说明理由,若有,请求出最大值.
-
科目: 来源: 题型:
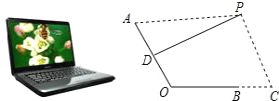
查看答案和解析>>【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据:
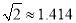 ,
, 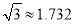 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( )
①等腰三角形两边长为2和5,则它的周长是9或12;②无理数-
 在-2和-1之间;③六边形的内角和是外角和的2倍;④若a>b,则a-b>0.它的逆命题是假命题;⑤北偏东30°与南偏东50°的两条射线组成的角为80°.
在-2和-1之间;③六边形的内角和是外角和的2倍;④若a>b,则a-b>0.它的逆命题是假命题;⑤北偏东30°与南偏东50°的两条射线组成的角为80°.A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
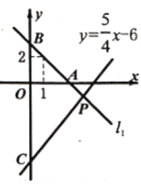
查看答案和解析>>【题目】如图,直线
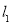 经过点
经过点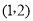 且与直线
且与直线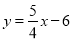 交于点
交于点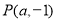 .
.
(1)求点
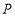 的坐标.
的坐标.(2)求直线
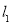 的表达式.
的表达式.(3)若直线
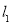 与
与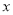 轴、
轴、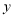 轴分别交于
轴分别交于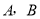 两点,直线
两点,直线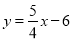 与
与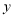 轴交于点
轴交于点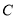 , 求
, 求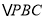 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在的直线折叠得到△AFE,延长AF交CD于点G,已知CG=2,DG=1,则BC的长是( )

A.3
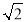 B.2
B.2 C.2
C.2 D.2
D.2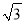
相关试题

