【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在的直线折叠得到△AFE,延长AF交CD于点G,已知CG=2,DG=1,则BC的长是( )

A.3![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
参考答案:
【答案】B
【解析】
连接EG,由折叠的性质可得BE=EF又由E是BC边的中点,可得EF=EC,然后证得Rt△EGF≌Rt△EGC(HL),得出FG=CG=2,继而求得线段AG的长,再利用勾股定理求解,即可求得答案.
解:连接EG,
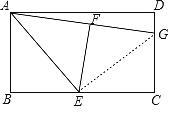
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EFG=∠B=90°,
∵在Rt△EGF和Rt△EGC中,
![]() ,
,
∴Rt△EGF≌Rt△EGC(HL),
∴FG=CG=2,
∵在矩形ABCD中,AB=CD=CG+DG=2+1=3,
∴AF=AB=3,
∴AG=AF+FG=3+2=5,
∴BC=AD=![]() =
=![]() =2
=2![]() .
.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.设租用时间为
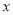 个月,所需租金为
个月,所需租金为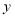 元.
元.(1)请分别写出租用甲、乙两家房屋的租金
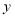 与租用时间
与租用时间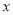 之间的函数关系;
之间的函数关系;(2)试判断租用哪家房屋更合算,请写出详细分析过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( )
①等腰三角形两边长为2和5,则它的周长是9或12;②无理数-
 在-2和-1之间;③六边形的内角和是外角和的2倍;④若a>b,则a-b>0.它的逆命题是假命题;⑤北偏东30°与南偏东50°的两条射线组成的角为80°.
在-2和-1之间;③六边形的内角和是外角和的2倍;④若a>b,则a-b>0.它的逆命题是假命题;⑤北偏东30°与南偏东50°的两条射线组成的角为80°.A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
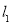 经过点
经过点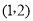 且与直线
且与直线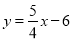 交于点
交于点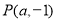 .
.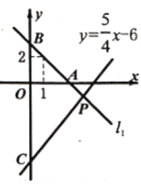
(1)求点
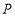 的坐标.
的坐标.(2)求直线
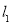 的表达式.
的表达式.(3)若直线
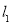 与
与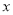 轴、
轴、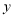 轴分别交于
轴分别交于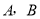 两点,直线
两点,直线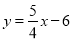 与
与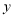 轴交于点
轴交于点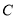 , 求
, 求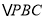 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
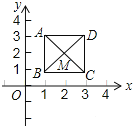
A. (﹣2012,2)B. (﹣2012,﹣2)C. (﹣2013,﹣2)D. (﹣2013,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC与BD相交于点O.要使四边形ABCD是正方形,还需添加一组条件.下面给出了五组条件:①AB=AD,且AC=BD;②AB⊥AD,且AC⊥BD;③AB⊥AD,且AB=AD;④AB=BD,且AB⊥BD;⑤OB=OC,且OB⊥OC.其中正确的是_____(填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:﹣4,|﹣2|,﹣2,﹣(﹣3.5),0,
 .
.(1)在如图所示的数轴上表示出以上各数;

(2)比较以上各数的大小,用“<”号连接起来;
_____<_____<______<______<______<______
(3)在以上各数中选择恰当的数填在图中这两个圈的(重叠)部分.

相关试题

