【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
参考答案:
【答案】(1)甲材料每千克15元,乙材料每千克25元(2)三种方案(3)当m=22时,总成本最低,此时W=-200×22+55000=50600元
【解析】试题分析:(1)、首先设甲种材料每千克x元, 乙种材料每千克y元,根据题意列出二元一次方程组得出答案;(2)、设生产B产品a件,则A产品(60-a)件,根据题意列出不等式组,然后求出a的取值范围,得出方案;得出生产成本w与a的函数关系式,根据函数的增减性得出答案.
试题解析:(1)设甲种材料每千克x元, 乙种材料每千克y元,
依题意得: ![]() 解得:
解得: ![]()
答:甲种材料每千克25元, 乙种材料每千克35元.
(2)生产B产品a件,生产A产品(60-a)件. 依题意得:
![]() 解得:
解得: ![]()
∵a的值为非负整数 ∴a=39、40、41、42
∴共有如下四种方案:A种21件,B种39件;A种20件,B种40件;A种19件,B种41件;A种18件,B种42件
(3)、答:生产A产品21件,B产品39件成本最低.
设生产成本为W元,则W与a的关系式为:w=(25×4+35×1+40)(60-a)+(35×+25×3+50)a=55a+10500
∵k=55>0 ∴W随a增大而增大∴当a=39时,总成本最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
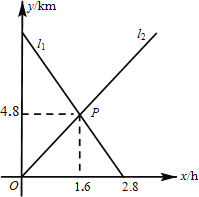
A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
-
科目: 来源: 题型:
查看答案和解析>>【题目】张勤同学的父母在外打工,家中只有年迈多病的奶奶.星期天早上,李老师从家中出发步行前往张勤家家访.6分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14分钟后以相同的速度按原路返回,结果与李老师同时到家.张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t(0≤t≤32)分钟后师生二人离张勤家的距离分别为S1、S2.S与t之间的函数关系如图所示,请你解答下列问题:
(1)李老师步行的速度为 ;
(2)求S2与t之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP和△ECP相似的是( )

A. ∠APB=∠EPC B. ∠APE=90° C. BP:BC=2:3 D. P是BC中点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.解答下列问题:
(1)当t为何值时,以点E、P、Q为顶点的三角形与△ADE相似?
(2)当t为何值时,△EPQ为等腰三角形?(直接写出答案即可);

-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣4x+4=0的根的情况是( )
A.有两个相等的实数根
B.只有一个实数根
C.没有实数根
D.有两个不相等的实数根 -
科目: 来源: 题型:
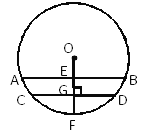
查看答案和解析>>【题目】如图,圆柱形水管内原有积水的水平面宽CD=10cm,水深GF=1cm,若水面上升1cm(EG=1cm),则此时水面宽AB为多少?
相关试题

