【题目】我省某工艺厂为全运会设计了一款成本为每件20元的工艺品,投放市场试销后发现每天的销售量y(件)是售价x(元/件)的一次函数。当售价为22元/件时,每天销售量为780件;当售价为25元/件时,每天销售量为750件。
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本)
参考答案:
【答案】
(1)
解:设y与x的函数关系式为y=kx+b(k≠0),
把x=22,y=780和x=25,y=750代入y=kx+b,得
![]()
解得![]()
∴y与x的函数关系式为y=-10x+1000.
(2)
解:设该工艺品每天获得的利润为w元,
则w=y(x-20)=(-10x+1000)(x-20)=-10(x-60)2+16000,(20≤x≤100);
∵-10<0,
∴当20<x≤30时,w随x的增大而增大.
所以当售价定为30元/件时,该工艺品每天获得的利润最大.
W最大=-10(30-60)2+16000=7000元.
答:当售价定为30元/时,该工艺品每天获得的利润最大,最大利润为7000元.
【解析】(1)y与x是一次函数,则可设y=kx+b,运用待定系数法求;
(2)设该工艺品每天获得的利润为w元,根据总利润=销售量×单件利润,列出w关于x的函数解析式,由x的取值范围,讨论x为何值时,w最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为
 O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使
O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使  PED=
PED=  C.
C.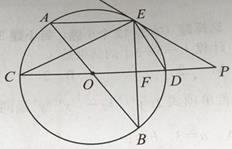
(1)求证:PE是 O的切线;
O的切线;
(2)求证:ED平分 BEP;
BEP;
(3)若 O的半径为5,CF=2EF,求PD的长.
O的半径为5,CF=2EF,求PD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距 千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
(5)若B的自行车不发生故障,保持出发时的速度前进, 小时与A相遇,相遇点离B的出发点 千米.在图中表示出这个相遇点C.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面算式,解答问题:
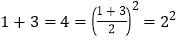
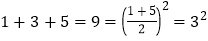
 ……
……(1)请求出1 3 5 7 9 11的结果为 ;
请求出1 3 5 7 9 29 的结果为 ;
(2)若n 表示正整数,请用含 n 的代数式表示1 3 5 7 9 (2n 1) (2n 1) 的值为
(3)请用上述规律计算: 41 43 45 77 79 的值(要求写出详细解答过程).
-
科目: 来源: 题型:
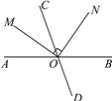
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示:

(1)求y关于x的函数解析式,并写出它的定义域;
(2)当王阿姨销售草莓获得的利润为800元时,求草莓销售的单价. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6
 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)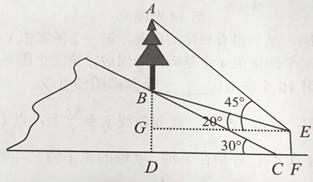
相关试题

