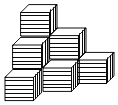
【题目】棱长为a的正方体,摆放成如图所示的形状,动手试一试,并回答下列问题:
(1)如果这一物体摆放了如图所示的上下三层,由几个正方体构成?
(2)如图形所示物体的表面积是多少?
参考答案:
【答案】(1)由10个正方体构成;(2)如图形所示物体的表面积是36a2平方单位.
【解析】
(1) 观察已知图形,不难得到每一层上正方体的个数,即可得出正确答案;
(2) 由于每个小正方体的棱长为![]() ,即可得到每个小正方形的面积,根据所观察的三视图去求其面积大小.
,即可得到每个小正方形的面积,根据所观察的三视图去求其面积大小.
解:(1)第一层 1个,第一层 3个,第一层6个,
![]() (个).
(个).
答:由10个正方体构成;
(2)每个正方形面积为![]() ,左面:6小正方形,前面:6小正方形,
,左面:6小正方形,前面:6小正方形,
右面:6小正方形,后面:6小正方形,上面:6小正方形,下面:6小正方形.
物体的表面积为:![]() (平方单位).
(平方单位).
答:如图形所示物体的表面积是![]() 平方单位.
平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
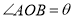 ,过点O作
,过点O作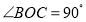 .
.(1)若
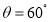 ,求
,求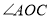 的度数;
的度数;(2)已知射线
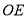 平分
平分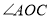 ,射线
,射线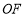 平分
平分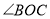 .
.①若
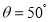 ,求
,求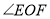 的度数;
的度数;②若
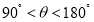 ,则
,则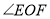 的度数为 (直接填写用含
的度数为 (直接填写用含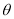 的式子表示的结果).
的式子表示的结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=
 t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+
 (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线
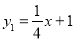 与
与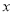 轴交于点
轴交于点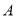 ,与
,与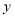 轴交于点
轴交于点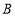 ,与反比例函
,与反比例函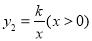 的图象交于点
的图象交于点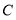 ,且
,且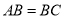 .
.(1)求点
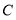 的坐标和反比例函数
的坐标和反比例函数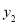 的解析式;
的解析式;(2)点
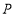 在
在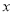 轴上,反比例函数
轴上,反比例函数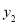 图象上存在点
图象上存在点 ,使得四边形
,使得四边形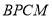 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.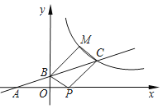
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>
 ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t< )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应承办“绿色奥运”的号召,九年级(1)班全体师生义务植树300棵.原计划每小时植树x棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,结果提前20分钟完成任务.则下面所列方程中,正确的是( )
A.
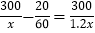 B.
B. 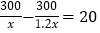
C.
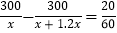 D.
D. 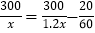
相关试题

