【题目】已知![]() ,过点O作
,过点O作![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)已知射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .
.
①若![]() ,求
,求![]() 的度数;
的度数;
②若![]() ,则
,则![]() 的度数为 (直接填写用含
的度数为 (直接填写用含![]() 的式子表示的结果).
的式子表示的结果).
参考答案:
【答案】(1)150°或30°;(2)①25°,②![]() θ或180°-
θ或180°-![]() θ
θ
【解析】
(1)分两种情形画出图形求解即可;
(2)①分两种情形画出图形分别求解即可;②分两种情形分别画出图形分别求解即可.
解:(1)如图1中,∠AOC=∠AOB+∠BOC=150°,
如图2中,∠AOC=∠BOC-∠AOB=30°.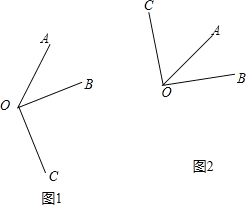
(2)①如图1-1中,∵∠AOC=∠AOB+∠BOC=140°,
∴∠EOC=![]() ∠AOC=70°,
∠AOC=70°,
∵∠FOC=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠EOC-∠FOC=25°,
如图2-1中,∵∠AOC=∠BOC-∠AOB=40°,
∴∠EOC=![]() ∠AOC=20°,
∠AOC=20°,
∵∠FOC=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠FOC-∠EOC=25°.

②如图1-2中,∵∠AOC=∠AOB-∠BOC=θ -90°,
∴∠EOC=![]() ∠AOC=
∠AOC=![]() (θ-90°),
(θ-90°),
∵∠FOC=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠EOC+∠FOC=![]() θ,
θ,
如图2-2中,∵∠AOC=360°-∠AOB-∠BOC=270°-θ
∴∠EOC=![]() ∠AOC=
∠AOC=![]() (270-θ),
(270-θ),
∵∠FOC=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠EOC+∠FOC=180°-![]() θ,
θ,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(
 ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).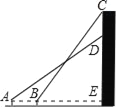
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 与函数
与函数 的图象交于
的图象交于 ,
,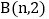 两点,
两点,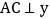 轴于C,
轴于C,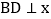 轴于D
轴于D 求k的值;
求k的值;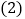 根据图象直接写出
根据图象直接写出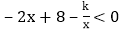 的x的取值范围;
的x的取值范围; 是线段AB上的一点,连接PC,PD,若
是线段AB上的一点,连接PC,PD,若 和
和 面积相等,求点P坐标.
面积相等,求点P坐标.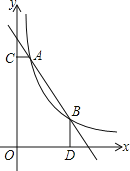
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
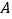 在数轴上对应的数为
在数轴上对应的数为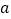 ,点
,点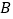 对应的数为
对应的数为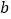 ,且
,且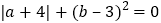 .
.
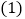 则
则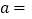 ________,
________,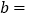 ________;并将这两个数在数轴上所对应的点
________;并将这两个数在数轴上所对应的点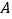 ,
,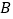 表示出来;
表示出来;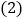 数轴上在
数轴上在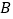 点右边有一点
点右边有一点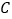 到
到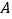 、
、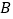 两点的距离和为
两点的距离和为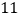 ,若点
,若点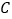 的数轴上所对应的数为
的数轴上所对应的数为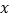 ,求
,求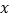 的值;
的值;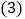 若点
若点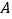 ,点
,点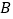 同时沿数轴向正方向运动,点
同时沿数轴向正方向运动,点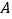 运动的速度为
运动的速度为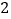 单位/秒,点
单位/秒,点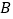 运动的速度为
运动的速度为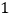 单位/秒,若
单位/秒,若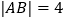 ,求运动时间
,求运动时间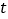 的值.
的值.(温馨提示:
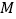 、
、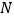 之间距离记作
之间距离记作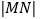 ,点
,点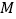 、
、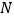 在数轴上对应的数分别为
在数轴上对应的数分别为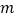 、
、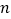 ,则
,则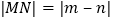 .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=
 t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+
 (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线
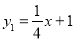 与
与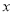 轴交于点
轴交于点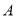 ,与
,与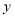 轴交于点
轴交于点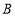 ,与反比例函
,与反比例函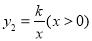 的图象交于点
的图象交于点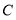 ,且
,且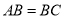 .
.(1)求点
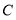 的坐标和反比例函数
的坐标和反比例函数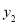 的解析式;
的解析式;(2)点
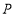 在
在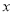 轴上,反比例函数
轴上,反比例函数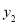 图象上存在点
图象上存在点 ,使得四边形
,使得四边形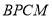 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.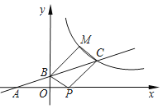
-
科目: 来源: 题型:
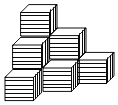
查看答案和解析>>【题目】棱长为a的正方体,摆放成如图所示的形状,动手试一试,并回答下列问题:
(1)如果这一物体摆放了如图所示的上下三层,由几个正方体构成?
(2)如图形所示物体的表面积是多少?
相关试题

